Mô tả vấn đề

Có ~ N ~ thị trấn ở Vương quốc Takahashi. Chúng được đánh số ~ 1 ~ đến ~ N ~.

Nhà vua Takahashi đang có kế hoạch đi thị sát trong ~ M ~ ngày. Anh ta sẽ xác định một chuỗi các thị trấn ~ c ~, và đến thăm thị trấn ~ c_i ~ vào ngày thứ ~ i ~. Tức là, vào ngày thứ ~ i ~, anh ấy sẽ đi từ vị trí hiện tại của mình đến thị trấn ~ c_i ~. Nếu anh ấy đã ở thị trấn rồi ~ c_i ~, anh ấy sẽ ở lại thị trấn đó. Vị trí của anh ấy ngay trước khi bắt đầu chuyến tham quan là thị trấn ~ 1 ~, thủ đô. Chuyến tham quan kết thúc tại thị trấn ~ c_M ~ mà không cần quay lại thủ đô.

Vấn đề là không có con đường trải nhựa ở vương quốc này. Anh quyết định giải quyết vấn đề này bằng cách tự mình mở đường khi đi du lịch. Khi anh ta đi từ thị trấn ~ a ~ đến thị trấn ~ b ~, sẽ có một con đường một chiều mới được trải nhựa từ thị trấn ~ a ~ đến thị trấn ~ b ~.

Vì anh ấy quan tâm đến người dân của mình, anh ấy muốn điều kiện sau được thỏa mãn sau khi chuyến hành trình của anh ấy kết thúc: "có thể đi từ bất kỳ thị trấn nào đến bất kỳ thị trấn nào khác bằng cách đi qua những con đường do anh ấy trải nhựa". Có bao nhiêu chuỗi ~ c ~ thỏa mãn điều kiện này?

Hạn chế

• ~ 2 ≤ N ≤ 300 ~
• ~ 1 ≤ M ≤ 300 ~

Input

Đầu vào được cung cấp theo định dạng sau:

~ N ~ ~ M ~

Output

In số chuỗi các thị trấn thỏa mãn điều kiện, modulo ~ 1000000007 (= 10 ^ 9 + 7) ~.

Đầu vào Mẫu 1

3 3

Đầu ra Mẫu 1

2

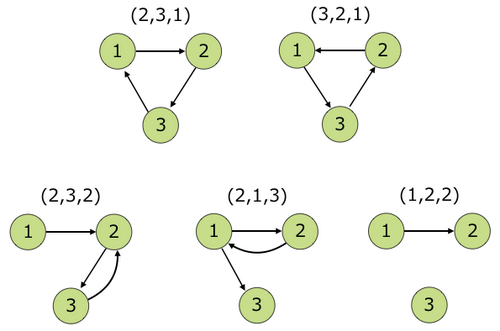
Như hình dưới đây, điều kiện chỉ được thỏa mãn khi ~ c = (2,3,1) ~ hoặc ~ c = (3,2,1) ~. Các dãy như ~ c = (2,3,2) ~, ~ c = (2,1,3) ~, ~ c = (1,2,2) ~ không thỏa mãn điều kiện.

Đầu vào Mẫu 2

150 300

Đầu ra Mẫu 2

734286322

Đầu vào Mẫu 3

300 150

Đầu ra mẫu 3

0