Mô tả vấn đề

Chúng ta có một đồ thị với ~ N ~ đỉnh, được đánh số từ ~ 0 ~ đến ~ N-1 ~. Các cạnh vẫn chưa được thêm vào.

Chúng tôi sẽ xử lý các truy vấn ~ Q ~ để thêm các cạnh. Trong truy vấn ~ i ~ -th ~ (1 ≤ i ≤ Q) ~, ba số nguyên ~ A_i, B_i ~ và ~ C_i ~ sẽ được đưa ra và chúng ta sẽ thêm vô số cạnh vào biểu đồ như sau:

• Hai đỉnh được đánh số ~ A_i ~ và ~ B_i ~ sẽ được nối với nhau bằng một cạnh có trọng số là ~ C_i ~.
• Hai đỉnh được đánh số ~ B_i ~ và ~ A_i + 1 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 1 ~.
• Hai đỉnh được đánh số ~ A_i + 1 ~ và ~ B_i + 1 ~ sẽ được nối với nhau bởi một cạnh có trọng số ~ C_i + 2 ~.
• Hai đỉnh được đánh số ~ B_i + 1 ~ và ~ A_i + 2 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 3 ~.
• Hai đỉnh được đánh số ~ A_i + 2 ~ và ~ B_i + 2 ~ sẽ được nối với nhau bởi một cạnh có trọng số ~ C_i + 4 ~.
• Hai đỉnh được đánh số ~ B_i + 2 ~ và ~ A_i + 3 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 5 ~.
• Hai đỉnh được đánh số ~ A_i + 3 ~ và ~ B_i + 3 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 6 ~.
• ...

Ở đây, hãy xem xét các chỉ số của các đỉnh modulo ~ N ~. Ví dụ, đỉnh được đánh số ~ N ~ là một được đánh số ~ 0 ~, và đỉnh được đánh số ~ 2N-1 ~ là một được đánh số ~ N-1 ~.

Hình dưới đây cho thấy bảy cạnh đầu tiên được thêm vào khi ~ N = 16, A_i = 7, B_i = 14, C_i = 1 ~:

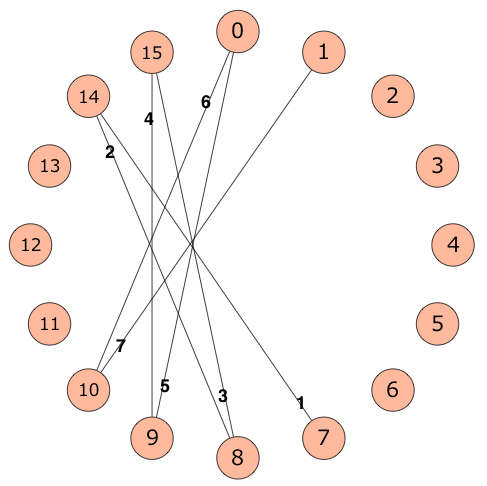
Sau khi xử lý tất cả các truy vấn, hãy tìm tổng trọng số của các cạnh có trong cây khung tối thiểu của đồ thị.

Hạn chế

• ~ 2 ≤ N ≤ 200.000 ~
• ~ 1 ≤ Q ≤ 200.000 ~
• ~ 0 ≤ A_i, B_i ≤ N-1 ~
• ~ 1 ≤ C_i ≤ 10 ^ 9 ~

Input

Đầu vào được cung cấp từ Đầu vào chuẩn ở định dạng sau:

~ N ~ ~ Q ~

~ A_1 ~ ~ B_1 ~ ~ C_1 ~

~ A_2 ~ ~ B_2 ~ ~ C_2 ~

~ A_Q ~ ~ B_Q ~ ~ C_Q ~

Output

In tổng trọng lượng của các cạnh có trong cây khung tối thiểu của biểu đồ.

Đầu vào Mẫu 1

7 1
5 2 1

Đầu ra Mẫu 1

21

Hình dưới đây cho thấy cây khung tối thiểu của biểu đồ:

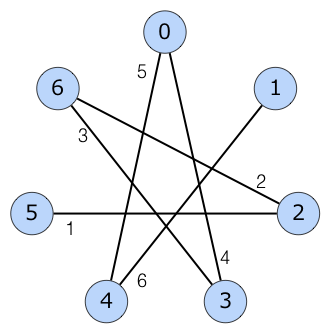
Lưu ý rằng có thể có nhiều cạnh nối cùng một cặp đỉnh.

Đầu vào Mẫu 2

2 1
0 0 1000000000

Đầu ra Mẫu 2

1000000001

Cũng lưu ý rằng có thể có các vòng lặp tự.

Đầu vào Mẫu 3

5 3
0 1 10
0 2 10
0 4 10

Đầu ra mẫu 3

42