Điểm khác biệt duy nhất giữa bản dễ và bản khó của bài toán là giới hạn của ~N~.

Ở những nơi tuyết rơi quanh năm như cực Bắc, hình dạng của những bông tuyết không khỏi khiến bản chất tò mò của các nhà nghiên cứu nơi đây trỗi dậy. Từ cửa sổ của trạm nghiên cứu, Minh nhìn những bông tuyết lục giác rơi khi cậu chợt nghĩ rằng, tại sao một bông tuyết lại phải là ~6~-giác mà không phải là ~k~-giác bất kỳ? Thế là cậu xây dựng một mô hình toán học để miêu tả các bông tuyết ~k~-giác như sau:

• Bắt đầu dựng bông tuyết từ ~1~ ngọn duy nhất.
• Sau đó, từ ngọn đầu tiên nối vào nó thêm ~k~ ngọn và lặp lại bước này với mỗi ngọn được thêm. Để hình dạng dựng nên trông như một bông tuyết thực sự, bước này được lặp lại ít nhất ~2~ lần và với ~k > 1~.

Bên dưới là một bông tuyết ~4~-giác với kích thước tối thiểu:

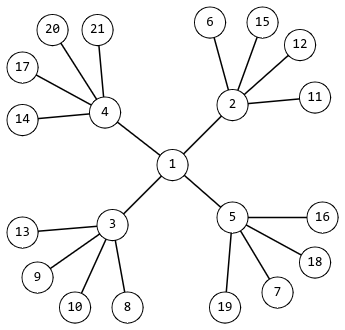
Để có thể hình dung được bông tuyết, cậu liền mang ~N~ con hải cẩu trong trạm của mình ra để xếp thử, nhưng với quy luật trên thì đôi khi một số lượng ngọn sẽ không thể dựng được một bông tuyết hoàn chỉnh. Liệu với ~N~ con hải cẩu Minh có thể dựng được một bông tuyết ~k~-giác hoàn chỉnh nào hay không?

Input

• Dòng đầu tiên gồm số nguyên dương ~Q~ (~1 \leq Q \leq 10^4~) là số lượng truy vấn bạn cần trả lời.
• ~Q~ dòng tiếp theo, mỗi dòng ghi một số nguyên dương ~N~ duy nhất (~1 \leq N \leq 10^6~).

Output

Gồm ~Q~ dòng, với mỗi dòng ghi YES hoặc NO là câu trả lời cho truy vấn đó.

Sample input

9
1
2
3
6
13
15
255
10101
1000000

Sample output

NO
NO
NO
NO
YES
YES
YES
YES
NO

Subtask

• ~30\%~ số test có ~1 \leq N \leq 10^3~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.