Sau những chuyến đi công tác xa nhà, thầy Luna đã mua một thanh socola kích thước ~2 \times n~ về tặng các học trò ở CLB H3.2PL. Thầy muốn cắt nó ra thành các thanh socola hình chữ nhật kích thước tuỳ ý nhưng phải có chiều dài và rộng là các số nguyên. Thầy thắc mắc là có tất cả mấy cách cắt, bạn hãy giúp thầy nhé.

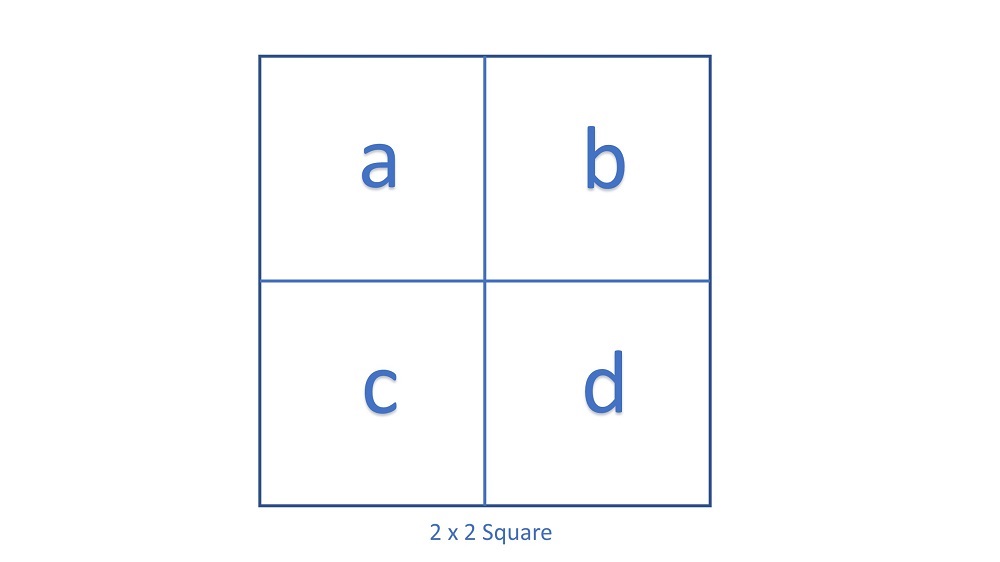
Chẳng hạn với ~n=1~ thì có thể giữ nguyên hoặc cắt làm đôi, có tất cả ~2~ cách. Còn với ~n=2~, để dễ hình dung, trong ảnh bên dưới, ta có các cách cắt sau đây: ~[(a,b,c,d)]~, ~[(a,b),(c,d)]~, ~[(a,c),(b,d)]~, ~[(a),(b),(c,d)]~, ~[(a,b),(c),(d)]~, ~[(a,c),(b),(d)]~, ~[(a),(c),(b,d)]~, ~[(a),(b),(c),(d)]~.

Input

Một số nguyên dương ~n~ duy nhất với ~1 \le n \le 10^{18}.~

Output

Số cách cắt cần tìm, lấy modulo ~10^9+7.~

Sample input 1

2

Sample output 1

8

Sample input 2

14

Sample output 2

412433792

Giới hạn

• Có 25% số test với ~n \le 20~.
• Có 50% số test ứng với ~21 < n \le 10^6~.
• Có 25% số test ứng với ~10^6 < n \le 10^{18}.~