IUHCoder Contest Round 5

Time limit: 2.0s / Memory limit: 1G

Points: 100

Problem Statement

Bạn có một dãy số nguyên A có chiều dài là N . Tìm sự khác biệt giữa hiệu số tối đa của 2 yếu tố (với các chỉ số khách nhau ) trong ~A~ .

Ràng buộc
  • ~2 \leq N \leq 100~
  • ~1 \leq A_i \leq 10^9~
  • Tất cả các giá trị đầu vào là số nguyên.
Input

Đầu vào tiêu chuẩn theo định dạng sau:

~N~

~A_1~ ~A_2~ ~...~ ~A_N~

Output

In ra sự khác biệt giữa hiệu số tối đa của 2 yếu tố (với các chỉ số khách nhau ) trong ~A~ .

Sample Input 1
4
1 4 6 3
Sample Output 1
5

Sự khác biệt hiệu số tối đa giữa 2 phần tử: ~A_3-A_1=6-1=5~ .

Sample Input 2
2
1000000000 1
Sample Output 2
999999999
Sample Input 3
5
1 1 1 1 1
Sample Output 3
0
Time limit: 2.0s / Memory limit: 1G

Points: 100

Problem Statement

Snuke có một chuỗi số nguyên ~A~ với chiều dài ~N~ .

Anh ấy tự do chọn số nguyên ~b~ . Ở đây, anh ta sẽ cảm thấy buồn nếu ~A_i~ và ~b+i~ cách xa nhau. Cụ thể hơn, the sadness của Snuke được tính như sau:

  • ~abs(A_1 - (b+1)) + abs(A_2 - (b+2)) + ... + abs(A_N - (b+N))~

Ở đây, ~abs(x)~ là một hàm trả về giá trị tuyệt đối của ~x~ .

Tìm nổi buồn tối thiểu của Snuke.

Ràng buộc
  • ~1 \leq N \leq 2 \times 10^5~
  • ~1 \leq A_i \leq 10^9~
  • Tất cả các giá trị đầu vào là số nguyên.
Input

Đầu vào tiêu chuẩn theo định dạng sau:

~N~

~A_1~ ~A_2~ ~...~ ~A_N~

Output

In ra nỗi buồn tối thiểu của Snuke

Sample Input 1
5
2 2 3 5 5
Sample Output 1
2

Nếu chúng ta chọn ~b=0~ , thì nỗi buồn tối thiều của Snuke sẽ là ~abs(2-(0+1))+abs(2-(0+2))+abs(3-(0+3))+abs(5-(0+4))+abs(5-(0+5))=2~ . Không có bất kì sự lựa chọn ~b~ nào nhỏ hơn 2 vì vậy đáp án là 2.

Sample Input 2
9
1 2 3 4 5 6 7 8 9
Sample Output 2
0
Sample Input 3
6
6 5 4 3 2 1
Sample Output 3
18
Sample Input 4
7
1 1 1 1 2 3 4
Sample Output 4
6
Time limit: 2.0s / Memory limit: 1G

Points: 100

Problem Statement

Có ~N~ hòn đảo được xếp hàng từ tây sang đông, được kết nối bởi ~N-1~ cây cầu.

Cây cầu thứ ~i~ được kết nối với hòn đảo thứ ~i~ từ phía tây và hòn đảo thứ ~(i+1)~ từ phía tây.

Một ngày, tranh chấp đã diễn ra tại một số hòn đảo, và có ~M~ yêu cầu từ các cư dân của các hòn đảo

Yêu cầu thứ ~i~ : Tranh chấp hòn đảo thứ ~a_i~ từ phía tây và hòn đảo thứ ~b_i~ từ phía tây. Hãy làm cho việc di chuyển giữa các các cây cầu là không thể.

Bạn đã quyết định loại bỏ một sô cây cầu đáp ứng tất cả ~M~ yêu cầu.

Tìm số lượng cây cầu tối thiểu phải được gỡ bỏ.

Constraints
  • Tất cả các giá trị đầu vào là số nguyên
  • ~2 \leq N \leq 10^5~
  • ~1 \leq M \leq 10^5~
  • ~1 \leq a_i < b_i \leq N~
  • Tất cả các cặp ~(a_i, b_i)~ là riêng biệt.
Input

Đầu vào tiêu chuẩn theo định dạng sau:

~N~ ~M~

~a_1~ ~b_1~

~a_2~ ~b_2~

~:~

~a_M~ ~b_M~

Output

In ra số lượng cây cầu tối thiểu cần gỡ bỏ.

Sample Input 1
5 2
1 4
2 5
Sample Output 1
1

Các yêu cầu có thể được đáp ứng bằng cách loại bỏ cây cầu nối các đảo thứ hai và thứ ba từ phía tây.

Sample Input 2
9 5
1 8
2 7
3 5
4 6
7 9
Sample Output 2
2
Sample Input 3
5 10
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5
Sample Output 3
4
Time limit: 2.0s / Memory limit: 1G

Points: 100

Problem Statement

Snuke có một chuỗi số nguyên ~A~ có chiều dài ~N~ .

Anh ấy sẽ thực hiện ba lần cắt giảm trong ~A~ và chia nó thành 4 (không rỗng) tiếp giáp với các chuỗi con ~B, C, D~ và ~E~ . Các vị trí các nút cắt có thể được tự do chọn.

Cho ~P,Q,R,S~ là tổng của các phần tử trong ~B,C,D,E~ , tương ứng. Snuke cảm thấy hạnh phúc khi sự khác biệt tuyệt đối của tối đa và tối thiểu giữa ~P,Q,R,S~ là nhỏ nhất. Tìm sự khác biệc tuyệt đối tối đa và tối thiểu giữa ~P,Q,R,S~

Ràng buộc
  • ~4 \leq N \leq 2 \times 10^5~
  • ~1 \leq A_i \leq 10^9~
  • Tất cả các giá trị đầu vào là số nguyên.
Input

Đầu vào tiêu chuẩn theo định dạng sau:

~N~

~A_1~ ~A_2~ ~...~ ~A_N~

Output

Tìm sự khác biệt tuyệt đối tối đa và tối thiểu giữa ~P,Q,R,S~

Sample Input 1
5
3 2 4 1 2
Sample Output 1
2

Nếu chúng chia cho ~A~ như ~B,C,D,E=(3),(2),(4),(1,2)~ , sau đó ~P=3,Q=2,R=4,S=1+2=3~ . Ở đây, giá trị tối đa và tối thiểu giữa ~P,Q,R,S~ là ~4~ và ~2~ , với sự khác biệt tuyệt đối là ~2~ . Chúng tôi không thể tạo ra sự khác biệt tuyệt đối của mức tối đa và mức tối thiểu nhỏ hơn 2 , vì vậy câu trả lời là 2.

Sample Input 2
10
10 71 84 33 6 47 23 25 52 64
Sample Output 2
36
Sample Input 3
7
1 2 3 1000000000 4 5 6
Sample Output 3
999999994
Time limit: 2.0s / Memory limit: 256M

Points: 100

Mô tả vấn đề

Chúng ta có một đồ thị với ~ N ~ đỉnh, được đánh số từ ~ 0 ~ đến ~ N-1 ~. Các cạnh vẫn chưa được thêm vào.

Chúng tôi sẽ xử lý các truy vấn ~ Q ~ để thêm các cạnh. Trong truy vấn ~ i ~ -th ~ (1 ≤ i ≤ Q) ~, ba số nguyên ~ A_i, B_i ~ và ~ C_i ~ sẽ được đưa ra và chúng ta sẽ thêm vô số cạnh vào biểu đồ như sau:

  • Hai đỉnh được đánh số ~ A_i ~ và ~ B_i ~ sẽ được nối với nhau bằng một cạnh có trọng số là ~ C_i ~.
  • Hai đỉnh được đánh số ~ B_i ~ và ~ A_i + 1 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 1 ~.
  • Hai đỉnh được đánh số ~ A_i + 1 ~ và ~ B_i + 1 ~ sẽ được nối với nhau bởi một cạnh có trọng số ~ C_i + 2 ~.
  • Hai đỉnh được đánh số ~ B_i + 1 ~ và ~ A_i + 2 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 3 ~.
  • Hai đỉnh được đánh số ~ A_i + 2 ~ và ~ B_i + 2 ~ sẽ được nối với nhau bởi một cạnh có trọng số ~ C_i + 4 ~.
  • Hai đỉnh được đánh số ~ B_i + 2 ~ và ~ A_i + 3 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 5 ~.
  • Hai đỉnh được đánh số ~ A_i + 3 ~ và ~ B_i + 3 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 6 ~.
  • ...

Ở đây, hãy xem xét các chỉ số của các đỉnh modulo ~ N ~. Ví dụ, đỉnh được đánh số ~ N ~ là một được đánh số ~ 0 ~, và đỉnh được đánh số ~ 2N-1 ~ là một được đánh số ~ N-1 ~.

Hình dưới đây cho thấy bảy cạnh đầu tiên được thêm vào khi ~ N = 16, A_i = 7, B_i = 14, C_i = 1 ~:

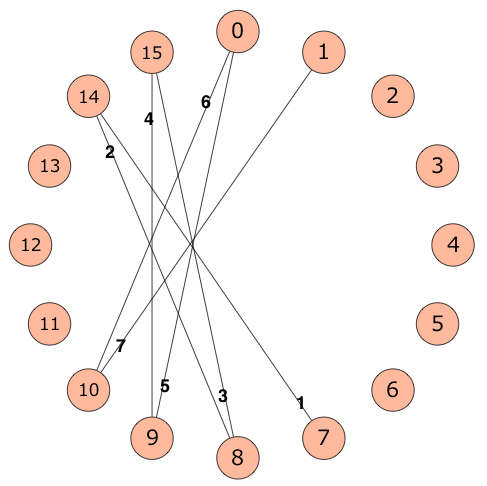
Sau khi xử lý tất cả các truy vấn, hãy tìm tổng trọng số của các cạnh có trong cây khung tối thiểu của đồ thị.

Hạn chế
  • ~ 2 ≤ N ≤ 200.000 ~
  • ~ 1 ≤ Q ≤ 200.000 ~
  • ~ 0 ≤ A_i, B_i ≤ N-1 ~
  • ~ 1 ≤ C_i ≤ 10 ^ 9 ~
Input

Đầu vào được cung cấp từ Đầu vào chuẩn ở định dạng sau:

~ N ~ ~ Q ~

~ A_1 ~ ~ B_1 ~ ~ C_1 ~

~ A_2 ~ ~ B_2 ~ ~ C_2 ~

~ A_Q ~ ~ B_Q ~ ~ C_Q ~

Output

In tổng trọng lượng của các cạnh có trong cây khung tối thiểu của biểu đồ.

Đầu vào Mẫu 1
7 1
5 2 1
Đầu ra Mẫu 1
21

Hình dưới đây cho thấy cây khung tối thiểu của biểu đồ:

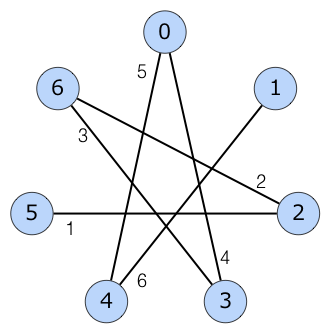
Lưu ý rằng có thể có nhiều cạnh nối cùng một cặp đỉnh.

Đầu vào Mẫu 2
2 1
0 0 1000000000
Đầu ra Mẫu 2
1000000001

Cũng lưu ý rằng có thể có các vòng lặp tự.

Đầu vào Mẫu 3
5 3
0 1 10
0 2 10
0 4 10
Đầu ra mẫu 3
42
Time limit: 2.0s / Memory limit: 256M

Points: 100

Mô tả vấn đề

Có ~ N ~ ô vuông liên tiếp, được đánh số từ ~ 1 ~ đến ~ N ~ từ trái sang phải. Snuke và Rng đang chơi trò chơi trên bàn cờ bằng cách sử dụng các ô vuông này, được mô tả dưới đây:

  1. Đầu tiên, Snuke viết một số nguyên vào mỗi ô vuông.
  2. Mỗi người trong hai người chơi sở hữu một mảnh. Snuke đặt quân cờ của mình vào ô vuông ~ 1 ~, và Rng đặt quân cờ vào ô vuông ~ 2 ~.
  3. Người chơi có quân cờ ở bên trái đối phương sẽ di chuyển quân cờ của mình. Đích đến phải là một hình vuông ở bên phải của hình vuông nơi quân cờ đang được đặt và không được vào hình vuông nơi quân cờ của đối thủ được đặt.
  4. Lặp lại bước 3. Khi các quân cờ không thể di chuyển được nữa, trò chơi kết thúc.
  5. Điểm của mỗi người chơi được tính bằng tổng các số nguyên được viết trong các ô vuông mà người chơi đã đặt quân cờ của mình trước khi kết thúc trò chơi.

Snuke đã viết một số nguyên ~ A_i ~ vào hình vuông ~ i (1 ≤ i ≤ N-1) ~, nhưng không viết vào hình vuông thứ ~ N ~. Anh ấy đã quyết định tính toán cho mỗi ~ M ~ số nguyên ~ X_1, X_2, ..., X_M ~, nếu anh ấy viết nó vào ô vuông ~ N ~ và trò chơi được chơi, giá trị Điểm của Snuke - Điểm của Rng sẽ được là bao nhiêu. Ở đây, người ta giả định rằng mỗi người chơi di chuyển quân cờ của mình để tối đa hóa giá trị điểm của người chơi - điểm của đối thủ.

Hạn chế
  • ~ 3 ≤ N ≤ 200.000 ~
  • ~ 0 ≤ A_i ≤ 10 ^ 6 ~
  • Tổng của tất cả ~ A_i ~ nhiều nhất là ~ 10 ^ 6 ~.
  • ~ 1 ≤ M ≤ 200.000 ~
  • ~ 0 ≤ X_i ≤ 10 ^ 9 ~
Đầu vào

Đầu vào được cung cấp theo định dạng sau:

~ N ~

~ A_1 ~ ~ A_2 ~ ~ ... ~ ~ A_ {N-1} ~

~ M ~

~ X_1 ~

~ X_2 ~

~: ~

~ X_M ~

Đầu ra

Đối với mỗi số nguyên ~ M ~ ~ X_1, ..., X_M ~, in ra giá trị "(Điểm của Snuke) - (Điểm của Rng)" nếu nó được viết thành ô vuông ~ N ~, một trên mỗi dòng.

Đầu vào Mẫu 1
5
2 7 1 8
1
2
Đầu ra Mẫu 1
0

Trò chơi diễn ra như sau, trong đó Sđại diện cho quân của Snuke vàR đại diện cho Rng.

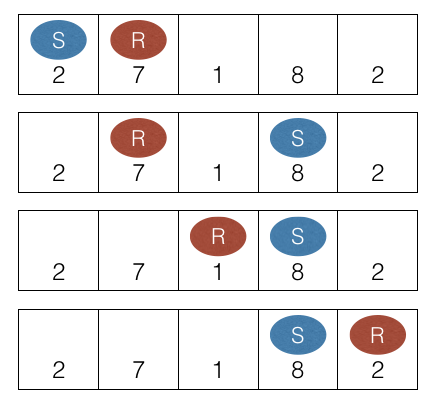
Điểm của cả hai người chơi là ~ 10 ~, do đó "(Điểm của Snuke) - (Điểm của Rng)" là ~ 0 ~.

Đầu vào Mẫu 2
9
2 0 1 6 1 1 2 6
5
2016
1
1
2
6
Đầu ra Mẫu 2
2001
6
6
7
7