Takahashi, người làm việc cho một nhà hàng pizza, đang làm một chiếc pizza phô mai thơm ngon cho bữa ăn nhân viên. Trước mặt anh có ~N~ loại phô mai khác nhau.

• Độ ngon của loại phô mai thứ ~i~ là ~A_i~ (tính theo mỗi gram).
• Có ~B_i~ gram phô mai của loại này.

Tổng độ ngon của pizza sẽ là tổng độ ngon của các loại phô mai được sử dụng trên chiếc pizza.

Để tránh lãng phí, chiếc pizza có thể chứa tối đa ~W~ gram phô mai. Hãy tìm độ ngon tối đa mà chiếc pizza có thể đạt được khi sử dụng các loại phô mai, với giới hạn là ~W~ gram.

Input

Dòng đầu tiên chứa hai số nguyên ~N~ và ~W~ (~1 \leq N \leq 3 \cdot 10^5, 1 \leq W \leq 3 \cdot 10^8~).

~N~ dòng tiếp theo mỗi dòng chứa hai số nguyên ~A_i~ và ~B_i~ tương ứng (~1 \leq A_i \leq 10^9, 1 \leq B_i \leq 10^3~).

Output

Ghi một số nguyên dương duy nhất là đáp án của bài toán.

Sample Input 1

3 5
3 1
4 2
2 3

Sample Output 1

15

Sample Input 2

4 100
6 2
1 5
3 9
8 7

Sample Output 2

100

Problem Statement

A function ~f(x)~ defined for non-negative integers ~x~ satisfies the following conditions.

• ~f(0) = 1~ .
• ~f(k) = f(\lfloor \frac{k}{2}\rfloor) + f(\lfloor \frac{k}{3}\rfloor)~ for any positive integer ~k~ .

Here, ~\lfloor A \rfloor~ denotes the value of ~A~ rounded down to an integer.

Find ~f(N)~ .

Constraints

• ~N~ is an integer satisfying ~0 \le N \le 10^{18}~ .

Input

The input is given from Standard Input in the following format:

~N~

Output

Print the answer.

Sample Input 1

2

Sample Output 1

3

We have ~f(2) = f(\lfloor \frac{2}{2}\rfloor) + f(\lfloor \frac{2}{3}\rfloor) = f(1) + f(0) =(f(\lfloor \frac{1}{2}\rfloor) + f(\lfloor \frac{1}{3}\rfloor)) + f(0) =(f(0)+f(0)) + f(0)= 3~ .

Sample Input 2

0

Sample Output 2

1

Sample Input 3

100

Sample Output 3

55

Một người dùng lần lượt tạo ~N~ folder trên máy họ, folder thứ ~i~ được đặt tên là ~S_i~ là một xâu chỉ bao gồm các chữ cái Latin. Do sẽ có những folder trùng tên, máy tính sẽ lưu tên các folder như sau:

• Nếu tên folder ~S_i~ chưa được dùng, máy tính sẽ lưu bằng tên đó.
• Ngoài ra, với ~X~ là số lần ~S_i~ đã xuất hiện trước đó, máy sẽ lưu folder đó dưới cái tên ~S_i~ ~+~ ~(X)~.

Cho ~N~ xâu được dùng làm tên folder, hãy cho biết tên của ~N~ folder này sau khi lưu.

Input

• Dòng đầu tiên gồm số nguyên dương ~N~ (~1 \leq N \leq 10^5~) duy nhất là số lượng xâu.
• ~N~ dòng tiếp theo, dòng thứ ~i~ là xâu ~S_i~ (~1 \leq |S_i| \leq 10~).

Output

Ghi ra ~N~ dòng, dòng thứ ~i~ là tên của folder thứ ~i~ sau khi lưu trên máy.

Sample input

5
newfile
newfile
newfolder
newfile
newfolder

Sample output

newfile
newfile(1)
newfolder
newfile(2)
newfolder(1)

Subtask

• ~30\%~ số test có ~1 \leq N \leq 100~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Cho mảng A gồm n phần tử. Hãy cho biết có bao nhiêu đoạn con liên tiếp có tổng chia hết cho x.

Input

Dòng đầu tiên gồm 2 số n và x (~ 1 \le n \le 10^5 , 1 \le x \le 10^9 ~).

Dòng thứ hai gồm n số nguyên ~A_1, A_2, ..., A_n~ (~ 1 \le a_i \le 10^9 ~) các phần tử của mảng A.

Output

Một dòng duy nhất là số đoạn con liên tiếp có tổng chia hết cho x.

Examples

Input

6 3
5 1 2 4 3 2 

Output

9 

Giải thích: Các đoạn con liên tiếp có tổng chia hết cho 3 là:

• [1, 2]
• [1, 4]
• [1, 5]
• [2, 3]
• [2, 6]
• [3, 4]
• [3, 5]
• [4, 6]
• [5, 5]

Bạn có biết rằng, cực từ Bắc không cố định tại một vị trí địa lý mà luôn dịch chuyển? Chuyện này tuy không liên quan lắm đến bạn, nhưng nó lại là rắc rối to lớn cho các nhà khoa học đang nghiên cứu tại cực Bắc.

Chuyện rằng, những la bàn tại các trạm nghiên cứu nơi đây đã cũ và chỉ có thể vận hành chính xác nếu các trục chính của nó nằm cùng hướng với cực từ. Những trục chính của nó bao gồm 4 hướng Đông - Tây - Nam - Bắc cùng 4 hướng phụ tạo thành góc ~45^\texttt{o}~ với 4 hướng chính. Với việc từ trường ngày càng thay đổi nhanh chóng vì biến đổi khí hậu, càng ngày càng nhiều trạm nghiên cứu sẽ không thể sử dụng la bàn được nữa.

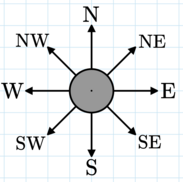
Để có thể lường trước được tình hình này, các nhà nghiên cứu cần phải tính trước số trạm có nguy cơ hỏng trong ~N~ trạm đang vận hành tại đây. Giả sử rằng cực từ luôn rơi vào toạ độ của một trạm nghiên cứu, với mỗi điểm rơi hãy tính số trạm vẫn có thể vận hành được la bàn (bao gồm cả trạm tại cực từ).

Input

• Dòng đầu tiên gồm số nguyên dương ~N~ (~1 \leq N \leq 10^5~) duy nhất là số lượng trạm nghiên cứu.
• ~N~ dòng tiếp theo, dòng thứ ~i~ ghi 2 số nguyên ~x_i~ và ~y_i~ (~-10^9 \leq x_i, y_i \leq 10^9~) là toạ độ của trạm nghiên cứu thứ ~i~.

Output

Ghi ra ~N~ số nguyên, mỗi số nguyên là số lượng trạm nghiên cứu vẫn hoạt động được nếu cực từ nằm ở đó.

Sample input

5
5 7
6 9
8 7
8 11
4 5

Sample output

2 3 4 3 1

Subtask

• ~30\%~ số test có ~1 \leq N \leq 1000~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Cho một tập hợp ~A~ rỗng và ~Q~ truy vấn, hãy xử lý từng truy vấn theo thứ tự. Mỗi truy vấn thuộc một trong ba dạng sau:

• ~1~ ~x~: Thêm giá trị vào tập hợp ~A~.

• ~2~ ~x~ ~k~: Trong các phần tử của ~A~ nhỏ hơn hoặc bằng ~x~, hãy in ra giá trị lớn thứ ~k~. (Giá trị của ~k~ không lớn hơn 5). Nếu có ít hơn ~k~ phần tử trong ~A~ nhỏ hơn hoặc bằng ~x~, in ra ~-1~.

• ~3~ ~x~ ~k~: Trong các phần tử của ~A~ lớn hơn hoặc bằng ~x~, hãy in ra giá trị nhỏ thứ ~k~. (Giá trị của ~k~ không lớn hơn 5). Nếu có ít hơn ~k~ phần tử trong ~A~ lớn hơn hoặc bằng ~x~, in ra ~-1~.

Input

Dòng đầu tiên chứa số nguyên ~Q~ ~(1 \leq Q \leq 2 \cdot 10^5)~.

~Q~ dòng tiếp theo, mỗi dòng chứa dạng truy vấn tương ứng ~(1 \leq x \leq 10^{18}, 1 \leq k \leq 5)~.

Ouput

Với truy vấn loại ~2, 3~ hãy in ra đáp án tương ứng.

Sample Input

11
1 20
1 10
1 30
1 20
3 15 1
3 15 2
3 15 3
3 15 4
2 100 5
1 1
2 100 5

Sample Output

20
20
30
-1
-1
1

Cho một mảng số nguyên vô tận phần tử, ban đầu mọi phần tử đều bằng ~0~. Bạn có ~Q~ truy vấn, mỗi truy vấn bạn sẽ phải tăng đoạn ~l~, ~r~ lên ~v~ đơn vị.

Hãy cho biết giá trị lớn nhất trong mảng và số lượng phần tử có giá trị đó sau ~Q~ truy vấn.

Input

• Dòng đầu tiên ghi số nguyên dương ~Q~ duy nhất (~1 \leq Q \leq 2 \cdot 10^5~) cho biết số lượng truy vấn bạn cần phải xử lý.
• ~Q~ dòng tiếp theo mỗi dòng ghi 3 số nguyên ~l~, ~r~ (~1 \leq l \leq r \leq 10^9~) và ~v~ (~1 \leq v \leq 10^9~).

Output

Ghi ra 2 số nguyên lần lượt là giá trị lớn nhất trong mảng và số lượng phần tử mang giá trị đó.

Sample input

5
1 2 1
1 6 4
3 8 5
4 7 1
2 5 3

Sample output

13 2

Subtask

• ~30\%~ số test có ~1 \leq l \leq r \leq 10^5~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Cảm thấy cư trú dài hạn ở Bắc cực quá khắc nghiệt và khó khăn, tiến sĩ Minh bèn bỏ việc nghiên cứu hải cẩu mà qua tìm hiểu lượng tử.

Tiến sĩ Minh cùng các nhà nghiên cứu tại đây đang tìm cách truyền thông điệp nhị phân sử dụng rối lượng tử, tuy nhiên việc truyền bằng những chiếc máy tính lượng tử chưa ổn định khiến tin liên tục bị nhiễu. Cụ thể hơn, họ đã truyền một xâu nhị phân gồm ~N~ bit, và họ đã truy được ~Q~ lần biến động lượng tử khiến 1 bit bất kỳ nào của xâu bị lật.

Để có thể đo lường được mức độ thay đổi, sau mỗi lần biến động họ sẽ đếm số lượng xâu 1100 xuất hiện trong thông điệp, nhưng với số lần nhiễu rất nhiều tiến sĩ Minh cùng cộng sự sẽ không thể đếm bằng tay hết được. Là thực tập sinh duy nhất trong phòng thí nghiệm mà biết lập trình, có lẽ chỉ có bạn mới giúp được họ.

Input

• Dòng đầu tiên ghi 2 số nguyên dương ~N~ và ~Q~ (~1 \leq N, Q \leq 10^5~) lần lượt là độ dài của xâu thông điệp ~S~ được truyền đi và số lần xâu bị nhiễu.
• Dòng thứ hai ghi một xâu nhị phân ~S~ độ dài ~N~.
• ~Q~ dòng tiếp theo, dòng thứ ~i~ lần lượt ghi số nguyên ~p_i~ (~1 \leq p_i \leq N~) cho biết vị trí bit mà thông điệp bị lật.

Output

Ghi ra ~Q~ số nguyên, mỗi dòng là số lần xâu 1100 xuất hiện trong thông điệp sau khi xâu bị thay đổi.

Sample input

8 3
11000000
5
6
4

Sample output

1
2
1

Subtask

• ~30\%~ số test có ~1 \leq N, Q \leq 1000~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Cho một mảng số nguyên ~A_1, A_2, \cdots, A_N~, bạn sẽ phải xử lý ~Q~ truy vấn có dạng sau:

• ~1~ ~l~ ~r~ - Với mỗi phần tử ~i~ từ ~l~ đến ~r~, đặt ~A_i~ bằng tổng các chữ số của nó.
• ~2~ ~x~ - Ghi ra giá trị của ~A_x~.

Input

• Dòng đầu tiên ghi số nguyên dương ~N~ duy nhất (~1 \leq N \leq 2 \cdot 10^5~) là số phần tử của mảng ~A~.
• Dòng thứ hai ghi ~N~ số, số thứ ~i~ là phần tử ~A_i~ của mảng (~1 \leq A_i \leq 10^9~).
• Dòng thứ ba ghi số nguyên dương ~Q~ là số lượng truy vấn bạn cần xử lý (~1 \leq Q \leq 2 \cdot 10^5~).
• ~Q~ dòng tiếp theo mỗi dòng là một truy vấn có 1 trong 2 dạng sau:
  • ~1~ ~l~ ~r~ (~1 \leq l \leq r \leq N~).
  • ~2~ ~x~ (~1 \leq x \leq N~).

Output

Với mỗi truy vấn loại 2, ghi ra một số nguyên là đáp án cho truy vấn đó trên mỗi dòng.

Sample input

5
1 420 69 1434 2023
8
1 2 3
2 2
2 3
2 4
1 2 5
2 1
2 3
2 5

Sample output

6
15
1434
1
6
7

Subtask

• ~30\%~ số test có ~1 \leq N, Q \leq 1000~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.