Bạn Tài và Lộc đang đi coi thầy phong thuỷ để xin quẻ cho một start up công nghệ. Năm trước, hai bạn đã khai trương và xin được một số phong thuỷ là ~n~ nhưng công ty vẫn còn nhiều khó khăn. Lần nay, thầy phong thuỷ phán rằng mỗi số ~n~ là chưa đủ mà hai bạn cần phải chi tiền ra xin thêm vài số nữa về dán thêm vào trong văn phong thì công ty sẽ ăn nên làm ra được. Các số đó, đặt là ~m~, có đặc điểm như sau:

• Đó là các số nguyên dương có giá trị không vượt quá ~n~;
• Là bình phương đúng hoặc lập phương đúng (tức là tồn tại ~x~ nguyên để ~m=x^2~ hoặc ~m=x^3~);
• Mỗi ước nguyên tố (nếu có) của ~m~ thì cũng là ước của ~n~?

Hãy giúp bạn Tài và Lộc tính xem họ cần dán bao nhiêu số theo lời thầy phong thuỷ nhé.

Input

Số nguyên dương ~n~ với ~1 \le n \le 10^{14}.~

Output

Số lượng số đặc biệt cần dán.

Sample input

36

Sample output

7

Giải thích.

Trong ví dụ đã cho, các số thỏa mãn là ~1, 4, 8, 9, 16, 27, 36~. Chú ý rằng số ~1~ vì không có ước nguyên tố nào nên tập ước nguyên tố của nó là tập rỗng, và cũng thoả mãn điều kiện.

Sau những ngày vất vả với các deadline ở trường thì Mạnh đã đăng ký tham gia chương trình mùa hè xanh cùng team. Mọi người sẽ cùng xuất phát tại TPHCM để đến ngọn đồi thiên lý, hoàn thành "hành trình nhật ký yêu thương đời mình". Tuy nhiên, Mạnh "ở vùng quê khu nghèo khó đó có trăm điều khó", vậy nên mọi thứ bạn phải rất tiết kiệm. Mạnh cùng đoàn mở bản đồ ra thì thấy có ~n~ địa điểm và ~m~ chặng đường một chiều nối giữa hai địa điểm nào đó (mỗi chặng đường sẽ có chi phí di chuyển nhất định), trong đó TPHCM có số thứ tự ~1~ còn địa điểm đích đến có số thứ tự ~n~. Cả đoàn được sử dụng thẻ sinh viên đúng một lần để giảm nửa giá vé của một chặng nào đó (từ giá ~a~ xuống còn giá ~[a/2]~). Hãy giúp Mạnh và team tính ra chi phí di chuyển ít nhất để họ sớm đến được ngọn đồi thiên lý nhé.

Input

Dòng đầu tiên có hai số nguyên ~n~ và ~m~, tương ứng là số lượng địa điểm trên bản đồ du lịch và số chặng, trong đó ~2 \leq n \leq 10^5~ và ~1 \leq m \leq 2.10^5~.

Tiếp theo là ~m~ dòng mô tả các chặng đường: mỗi dòng có ba số nguyên ~a,b~ và ~c~ mô tả một chặng bắt đầu tại địa điểm thứ ~a~, kết thúc tại địa điểm thứ ~b~ (với ~a \neq b~) và chi phí là ~c~, trong đó ~1 \leq a,b \leq n~ và ~1 \leq c \leq 10^9~.

Giả sử rằng luôn có thể đi từ TPHCM đến ngọn đồi thiên lý, đồng thời các cặp ~(a,b)~ không nhất thiết phân biệt nhau giữa các dòng.

Output

Một số nguyên là tổng chi phí cần sử dụng của team.

Sample input 1

2 2
1 2 5
1 2 6

Sample output 1

2

Sample Input 2

3 4
1 2 3
2 3 1
1 3 7
2 1 5

Sample Output 2

2

Giới hạn

• Có ~50\%~ số test ứng với ~1 \leq n \leq 20; 1 \leq m \leq 100~.
• Có ~50\%~ số test ứng với ~1 \leq n \leq 10^5; 1 \leq m \leq 2.10^5~.

Team IUH.CopyPaste là một team rất đặc biệt của ĐH Công Nghiệp HCM, đây là một team với sự kết hợp của 3 cá tính mạnh mẽ khác nhau:

• Đức Nam: một người thích màu hồng, yêu sự hoàn hảo.
• Văn Nhân: một người yêu màu xanh, thích chia cắt mọi thức.
• Chí Trung: đang tìm màu sắc yêu thích và quyết tâm làm mọi thứ đến cùng.

Với 3 tính cách như thế nên lúc làm bài không thể tránh khỏi có những suy nghĩ khác nhau, ví dụ như khi làm những bài Quy Hoạch Động:

• Đức Nam: thường có xu hướng nghĩ cách giải bằng việc đi giải các bài toán con trước sau đó dùng bài các bài toán con này để giải các bài toán lớn hơn.
• Văn Nhân: thì thường có xu hướng nghĩ cách giải bằng cách chia bài toán lớn thành các bài toán con nhỏ và đi giải các bài toán con này.
• Chí Trung: nghe ý tưởng của 2 đồng đội, implement chúng và submit.

Một ngày nọ, trong lúc đang train team cùng nhau về thuật toán Segment Tree với các truy vấn trong đoạn ~L, R~ trên một mảng ~A~ thì:

• Đức Nam: nếu sửa bài toán thành tìm chọn 2 số bất kỳ trong đoạn ~L, R~ và xét xem tích của chúng có là số chính phương hay không thì sao?
• Văn Nhân: quá dễ anh Nam (Nam là khóa trên của Trung và Nhân), nên cho bài toán là chia các số trong đoạn *~L, R~ * vào ~K~ nhóm sao cho:
  • ~K~ là số nhỏ nhất có thể
  • Mỗi số trong đoạn ~L, R~ phải thuộc đúng ~1~ nhóm trong ~K~ nhóm.
  • Nếu chọn ~2~ số bất kỳ trong một nhóm thì tích của chúng phải là một số chính phương.
• Đức Nam: Ok bài toán hay đó, Chí Trung code đi em.
• Chí Trung: Hmm em cũng thấy bài toán hay nên em sẽ để bài này lại cho contest "HTCPNVS #6" để các bạn làm, giờ mình đi ăn gà rán thôi.

Input

Dòng đầu tiên chứa ~2~ số nguyên ~N, Q~ ~(1 \leq N, Q \leq 3*10^5)~ là số lượng phần tử của mảng ~A~ và số lượng truy vấn.

Dòng tiếp theo chứa ~N~ số nguyên ~A_1, A_2,... A_N~ ~(0 \leq A_i \leq 10^7)~ tương ứng với từng phần tử của mảng ~A~.

~Q~ dòng truy vấn tiếp theo, mỗi dòng chứa ~2~ số nguyên ~L, R~ ~(1 \leq L \leq R \leq N)~.

Output

In ra ~Q~ dòng, với mỗi dòng một giá trị ~K~ là câu trả lời của truy vấn tương ứng.

Sample Input

7 2
2 8 0 3 7 20 5
1 4
4 6

Sample Output

2
3

CodeCamp là hoạt động thường niên của IUH hằng năm dành cho các bạn trong đội tuyển Olympic Tin Học của trường. Lần này, thầy Tình dẫn các bạn đội tuyển lập trại code ở cao nguyên Tà Nung tại một Homestay nằm giữa rừng thông tại Đà Lạt.

Mọi thứ của trại code đều thuận lợi cho đến buổi sáng của ngày train team ICPC thứ 4, một cơn gió mùa Đông thổi qua rừng thông và làm cáp mạng bị đứt, mọi hoạt động train team đều dừng lại.

Trong lúc buồn chán chẳng thể submit bài giải, Trung đã dùng máy tính gen ra một xâu chữ cái và yêu cầu Ban hãy cho biết số thao tác xóa tối thiểu để xóa toàn bộ ký tự của xâu hiện tại với điều kiện mỗi thao tác xóa Ban chỉ được chọn và xóa một xâu con gồm các ký tự liên tiếp và xâu con đó phải là xâu đối xứng.

Là một người thích làm các bài quy hoạch động hơn các bài xâu, chính vì thế Ban đã tìm đến sự giúp đỡ của bạn. Bạn hãy giải bài toán này giúp Ban nhé.

Input

Một dòng duy nhất chứa xâu ~S~ ~(1 \leq |S| \leq 500)~ chỉ gồm các ký tự từ ~a~ đến ~z~ là xâu ký tự mà Trung đã gen ra.

Output

Một số nguyên duy nhất là số thao tác xóa tối thiểu để Ban có thể xóa toàn bộ ký tự của xâu ~S~.

Sample Input 1

icpciuh

Sample Output 1

3

Sample Input 1

bankngu

Sample Output 1

5

Giải thích

Ở test case 2, ban đầu ta có xâu ~S = bankngu~ ta sẽ xóa xâu con ~nkn~ thì ta được ~S = bagu~ sau đó ta xóa từng ký tự xâu này.

Trong công ty đa cấp Trần Lộc, có tất cả ~n~ nhân sự đánh số từ ~1~ đến ~n~. Ban đầu cty chỉ có mỗi giám đốc Trần Lộc thôi (số thứ tự 1), sau đó Lộc mời thêm không quá ~2~ người vào. Mỗi người đó lại mời được thêm không quá ~2~ người nữa và cứ thế, cho đến hôm nay, công ty đã ăn nên làm ra với tổng cộng ~n~ nhân viên. Với một nhân viên ~X~ nào đó, những người được ~X~ mời trực tiếp là thế hệ thứ nhất của ~X~, rồi những người được những người đó mời vào là thế hệ thứ hai của ~X~ và cứ thế. Như vậy một người có thể tạo ra thêm ~0~ hoặc nhiều thế hệ. Tuy nhiên, giám đốc này thấy rằng nhân sự của công ty chưa có sự cân đối lắm, có người thì tạo được nhiều có người lại tạo được ít thế hệ.

Giám đốc Lộc muốn rằng với mỗi người ~Y~ bất kỳ trong công ty, nếu ~Y~ mời được ~Y_1,Y_2~ thì số thế hệ mà hai người này tạo ra chênh lệch không quá ~1~. Trong trường hợp nếu ~Y_1~ hoặc ~Y_2~ không tồn tại thì số thế hệ tạo được bởi người đó coi như là ~0~. Trong thời buổi kinh tế khó khăn, giám đốc Lộc muốn giảm bớt gánh nặng nhân sự nên muốn bỏ bớt vài người đi để yêu cầu trên được thỏa mãn. Hãy giúp giám đốc tính ra số lượng người cần bỏ đi ít nhất có thể.

Input

Dòng đầu tiên là số nhân viên ~n~ với ~1 \le n \le 2.10^5.~ Trong ~n-1~ dòng tiếp theo, mỗi dòng có một cặp số ~u,v~ cho biết người này được mời bởi người kia.

Output

Số nhân viên ít nhất cần bỏ đi.

Sample input 1

12
1 2
2 3
3 4
3 5
1 6
6 7
7 8
7 9
9 10
6 11
11 12

Sample output 1

3

Sample input 2

6
1 2
1 3
3 4
3 5
5 6

Sample output 1

1

Sau khi học về bài kiểm tra chuỗi đối xứng trên lớp, do chưa hiểu rõ nên bạn Phú đã lên mạng copy được thuật toán sau trên www.geeksforgeeks.org/ (đoạn code ở cuối bài). Hôm nay trong giờ ôn tập, thầy cho Phú một chuỗi ~s~ gồm các ký tự tiếng Anh in hoa, tuy nhiên chuỗi của thầy có thể không đối xứng nên nhanh chóng ngắt vòng lặp của thuật toán. Phú thì muốn vòng lặp chạy càng lâu càng tốt để bạn có thể debug, quan sát được quá trình chạy và hiểu rõ hơn. Bạn hãy giúp Phú xáo trộn chuỗi ~s~ lại để vòng lặp while có thể chạy được nhiều nhất nhé.

Input

Một chuỗi ký tự duy nhất có độ dài không quá ~10^5~ gồm các ký tự tiếng Anh in hoa.

Output

Số lần lặp nhiều nhất của vòng while.

Sample input

AABBCDEF

Sample output

3

Giải thích

Bạn có thể đảo chuỗi ~s~ lại thành ~ABCDEFBA~, chạy được qua hai vòng lặp đầu, đến vòng thứ ba mới ngắt.

bool isPalindrome(string str) {
    int low = 0;
    int high = str.size() - 1;
    while (low < high) {
        if (str[low] != str[high]) {
            return false; // not a palindrome.
        }
        low++; // move the low index forward
        high--; // move the high index backwards
    }
      return true; // is a palindrome     
}

Bạn được cho mảng hoán vị ~A~ gồm ~N~ phần tử được đặt trong một cái ống bán hình tròn như hình minh họa

Trong một thao tác bạn có thể lấy một phần tử ~A_i~ ~(1 \leq i \leq N)~ tại vị trí bất kỳ ra khỏi ống, nhưng bạn chỉ có thể thêm phần tử ~A_i~ vừa lấy đó vào ở tại ~2~ đầu ống.

Nhiệm vụ của bạn là hãy cho biết cần tối thiểu bao nhiêu thao tác trên để sắp xếp lại mảng ~A~ thành mảng tăng dần.

Input

Dòng đầu tiên chứa số nguyên dương ~N~ ~(1 \leq N \leq 10^6)~ là số lượng phần tử của mảng hoán vị ~A~.

Dòng thứ hai, chứa ~N~ số nguyên ~A_1, A_2,... A_N~ ~(1 \leq A_i \leq N)~ tương ứng với các phần tử của mảng hoán vị ~A~.

Output

Một số nguyên duy nhất là đáp án của bài toán.

Sample Input

4
1 3 2 4

Sample Output

2

Anh Ali Vũ có nuôi một đàn gồm ~n~ con bò sữa, mỗi con có một chuồng riêng. Tuy nhiên, đàn bò của anh rất kén ăn nên con nào cũng ốm yếu (xem trong ảnh), còn bỏ thừa cỏ: con thứ ~i~ đang bỏ thừa ~a_i~ đơn vị cỏ, giả sử đây là các số nguyên dương. Vì thế, một ngày nọ, anh đã bỏ đói chúng vài ngày rồi mới cho ăn: với độ đói bụng ~k~ là số nguyên dương, bò sẽ nhai lượng cỏ là ~k~ vừa đủ để hết đói bụng. Sau khi được anh Vũ nạp lại cỏ, lũ bò lại khá kén chọn, mỗi con chỉ bắt đầu ăn cỏ nếu số cỏ của chúng có là chia hết cho ~k~ (để ăn vừa hết trong vài lần nhai tiếp theo, không bỏ thừa nữa), số cỏ nào không chia hết thì bò lại tiếp tục nhịn, không thèm ăn. Hãy giúp anh Vũ chọn ra số ~k~ hợp lý để có ít nhất ~2~ con bò sẽ ăn cỏ và tổng lượng cỏ ăn được của các con bò là nhiều nhất nhé.

Input

Dòng đầu tiên ghi số nguyên dương ~n~ với ~2 \le n \le 2.10^5~, trong dòng thứ hai, ghi ~n~ số nguyên dương nằm trong phạm vi ~1,2,...,2.10^6~ (các số này không nhất thiết phân biệt).

Output

Số cỏ lớn nhất mà các con bò sẽ ăn nếu như anh Vũ bỏ đói chúng thích hợp.

Sample Input 1

3
2 3 5

Sample Output 1

3

Giải thích: anh Vũ sẽ bỏ đói các con bò với độ bỏ đói là ~1~, khi đó sẽ có ba con cùng ăn với tổng lượng cỏ là ~1 \times 3 = 3~; còn nếu bỏ đói với độ bỏ đói là ~5~ thì chỉ có con cuối là ăn cỏ, không thoả mãn điều kiện.

Sample Input 2

5
7 28 4 8 12

Sample Output 2

16

Giải thích : anh Vũ sẽ bỏ đói các con bò với độ bỏ đói là ~4~, khi đó sẽ có ~4~ con bò cuối ăn cỏ với tổng lượng ăn được là ~4 \times 4 = 16~, nếu anh Vũ bỏ đói chúng với độ bỏ đói là ~7~ thì hai con đầu sẽ ăn cỏ nhưng tổng lượng ăn được chỉ là ~2 \times 7 = 14~.

Team TripleK là măng non đầy tiềm năng của câu lạc bộ H3.2PL, gồm các coder sắp lên năm hai. Trong các công việc, họ rất chỉnh chu, nghiêm túc đến mức ai cũng mắc phải hội chứng ám ảnh về sự hoàn hảo (OCPD). Một ngày trong lúc sinh ra mảng số nguyên để test thuật toán đơn giản, họ thấy rằng các số sinh ra được chưa đẹp lắm: Khôi đi tính tổng các chữ số của mỗi số và Khang đổi nó ra hệ nhị phân, Kiệt thì muốn rằng số đổi ra được chỉ chứa đúng một chữ số ~1~, team sẽ coi số như thế là số OCPD. Chẳng hạn ~2024~ là số OCPD vì ~2+0+2+4=8~ và trong hệ nhị phân thì ~8=1000~, chỉ chứa có một chữ số ~1~.

Họ muốn tất cả ~n~ số họ sinh ra ban đầu đều phải OCPD nên nếu số nào chưa có tính chất này thì họ sẽ tăng số đang có lên ~1~ đơn vị và cứ làm như thế đến khi nào gặp được số OCPD đầu tiên thì thôi. Hãy giúp team TripleK tính xem họ cần thực hiện tổng cộng bao nhiêu lần cho mảng hiện tại nhé.

Input

Số nguyên dương ~n~ với ~1 \le n \le 10^5~, dòng tiếp theo gồm ~n~ số nguyên dương không vượt quá ~10^6.~

Output

Kết quả của bài toán.

Sample input

4
1 2 4 17

Sample output

0

Sample input

1
2023

Sample output

1

Giải thích: trong VD1, dễ thấy rằng khi tính tổng chữ số và đổi sang hệ nhị phân thì thu được: ~1,10,100,1000~, đều thoả mãn tiêu chí OCPD, vậy nên không cần làm gì cả. Còn trong VD2, số ~2023~ hiện tại chưa OCPD nhưng chỉ cần thêm ~1~ đơn vị nữa là được.

Sau những chuyến đi công tác xa nhà, thầy Luna đã mua một thanh socola kích thước ~2 \times n~ về tặng các học trò ở CLB H3.2PL. Thầy muốn cắt nó ra thành các thanh socola hình chữ nhật kích thước tuỳ ý nhưng phải có chiều dài và rộng là các số nguyên. Thầy thắc mắc là có tất cả mấy cách cắt, bạn hãy giúp thầy nhé.

Chẳng hạn với ~n=1~ thì có thể giữ nguyên hoặc cắt làm đôi, có tất cả ~2~ cách. Còn với ~n=2~, để dễ hình dung, trong ảnh bên dưới, ta có các cách cắt sau đây: ~[(a,b,c,d)]~, ~[(a,b),(c,d)]~, ~[(a,c),(b,d)]~, ~[(a),(b),(c,d)]~, ~[(a,b),(c),(d)]~, ~[(a,c),(b),(d)]~, ~[(a),(c),(b,d)]~, ~[(a),(b),(c),(d)]~.

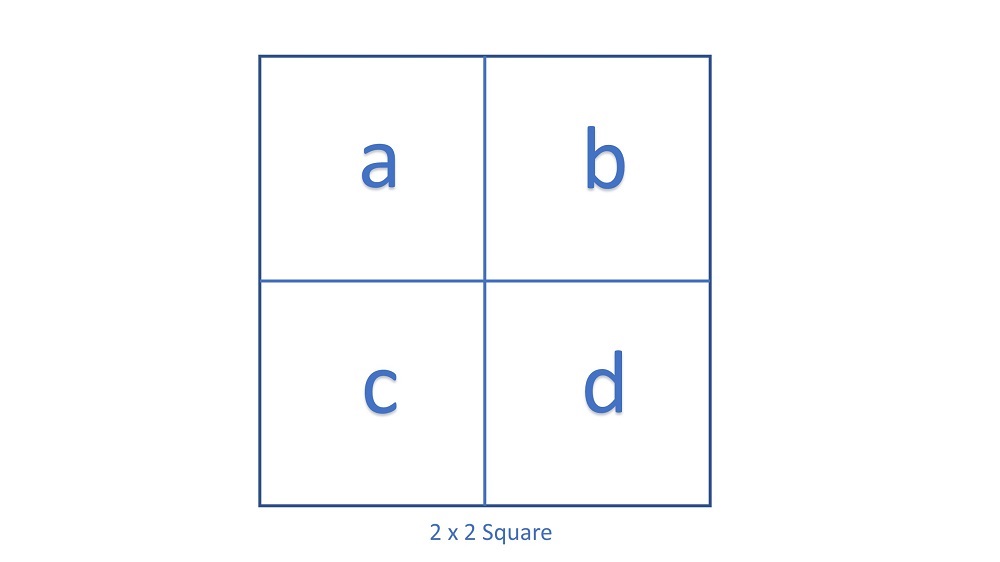
Input

Một số nguyên dương ~n~ duy nhất với ~1 \le n \le 10^{18}.~

Output

Số cách cắt cần tìm, lấy modulo ~10^9+7.~

Sample input 1

2

Sample output 1

8

Sample input 2

14

Sample output 2

412433792

Giới hạn

• Có 25% số test với ~n \le 20~.
• Có 50% số test ứng với ~21 < n \le 10^6~.
• Có 25% số test ứng với ~10^6 < n \le 10^{18}.~

Sau khi đã trải qua những áp lực, mệt mỏi trong cuộc sống, Mạnh đã dần tập chơi cây cảnh Bonsai để giải stress sau một ngày dài căng thẳng. Mỗi chậu cây Bonsai của Mạnh, anh ấy đều rất chăm chút và dán những con số đặc biệt lên các nhánh cây để lưu giữ các kỷ niệm với nó.

Cụ thể, chậu Bonsai của Mạnh được mô phỏng lại thành một cây có ~N~ đỉnh và tương ứng với ~N - 1~ cạnh mỗi cạnh sẽ có một trọng số ~W~ (là con số đặc biệt mà Mạnh đã dán lên). Thầy Tình sẽ truy vấn Mạnh ~Q~ câu hỏi, với mỗi câu hỏi sẽ là một trong 2 dạng:

1. Thầy Tình sẽ thay đổi giá trị trọng số của cạnh thứ ~m~ thành ~X~. Để tránh trường hợp Mạnh có thể đã học thuộc lòng các câu hỏi mà thầy Tình có thể hỏi.
2. Thầy Tình sẽ hỏi Mạnh kết quả khi XOR các giá trị trọng số trên đường đi từ ~u~ đến ~v~ là bao nhiêu?

Do đã quá mệt mỏi với việc học tập (hoặc có thể là do chậu Bonsai này không phải anh ấy tự trồng) nên anh ấy đã nhờ bạn đứng cạnh và nhắc anh ấy câu trả lời khi thầy Tình truy vấn. Bạn hãy làm một người tốt và giúp đỡ Mạnh nhé!

Input

Dòng đầu tiên chứa hai số nguyên ~N, Q~ ~(1 \leq N, Q \leq 100000)~ tương ứng với số đỉnh mô phỏng cây Bonsai và số truy vấn của* thầy Tình* đặt ra.

~N - 1~ dòng tiếp theo, mỗi dòng sẽ chứa ba số nguyên ~u, v, W~ ~(1 \leq u, v \leq N, 1 \leq W \leq 10^9)~ tương ứng với cạnh ~u, v~ sẽ có trọng số là ~W~.

~Q~ dòng tiếp theo, đầu tiên sẽ chứa số nguyên ~type~ ~(1 \leq type \leq 2)~ nếu:

• ~type = 1~, thì sẽ chứa tiếp theo hai số nguyên ~m, X~ ~(1 \leq m \leq N - 1, 1 \leq X \leq 10^9)~ tương ứng với truy vấn ~1~ của thầy Tình.
• ~type = 2~, thì sẽ chứa tiếp theo hai số nguyên ~u, v~ ~(1 \leq u, v \leq N)~ tương ứng với truy vấn ~2~ của thầy Tình.

Output

Với truy vấn ~2~ bạn hãy nhắc Mạnh kết quả của truy vấn tương ứng nhé.

Sample Input

5 3
1 2 2
1 3 3
2 4 5
3 5 7
2 4 5
1 1 9
2 4 5

Sample Output

3
8

Nhân dịp có nhiều cao thủ tham gia contest Hướng tới những vì sao lần đầu của năm 2024, BTC xin dành tặng bài cuối cùng này như một thử thách thú vị: Cho số nguyên dương ~n~ và số nguyên tố ~p < n~. Một số nguyên ~m~ với ~1 \le m \le n~ được gọi là tốt nếu như ~C_n^m~ chia hết cho ~p~. Đếm số lượng số tốt.

Ở đây, hệ số nhị thức ~C_n^m~ xác định bởi công thức ~\frac{n!}{m!(n-m)!}.~

Input

Một dòng duy nhất gồm số nguyên dương ~n~ và số nguyên tố ~p~, trong đó ~1 \le n \le 10^{18}~ và ~2 \le p \le \min \{100,n \}.~

Output

Một dòng duy nhất cho biết số lượng số tốt.

Sample input 1

16 2

Sample output 1

15

Sample input 2

20 19

Sample output 2

17

Subtasks

Trong Ví dụ 1, ta thấy các số tốt sẽ bao gồm ~1,2,...,15~. Trong Ví dụ 2, ta đếm được các số tốt là ~2,3,...,18.~

• Có ~25\%~ số test của đề ứng với ~n \le 100.~

• Có ~25\%~ số test của đề ứng với ~100 < n \le 10^5.~

• Có ~50\%~ số test của đề ứng với ~10^5 < n \le 10^{18}.~

(Nguồn bài: đề thi đề nghị Trại hè Hùng Vương 2023)

Ta gọi hai xâu ~X~ và ~Y~ là tương đồng bậc ~k~ nếu như chúng thoả mãn đồng thời:

i) Chúng có độ dài bằng nhau, tức là ~|X| = |Y|~;

ii) Ký tự ~X[i]~ và ~Y[i]~ cách nhau không quá ~k~ vị trí trong bảng mã ASCII với mọi ~i = 1, 2,.., |X|~.

Yêu cầu: Cho số nguyên ~k~ và 2 xâu ~S_1, S_2~ có độ dài bằng nhau (xâu chỉ gồm ký tự ~a~ đến ~z~). Hãy xác định số cách cắt ~S_1~ thành 3 xâu khác rỗng, sau đó ghép tạo thành xâu ~S_3~ mà xâu ~S_3~ tương đồng bậc ~k~ với xâu ~S_2~. Hai cách cắt được gọi là khác nhau nếu tồn tại một vị trí cắt khác nhau.

Input

Dòng 1: chứa số nguyên ~k~, còn dòng 2: chứa xâu ~S_1~ và dòng 3: chứa xâu ~S_2~.

Output

Số cách cắt thỏa mãn.

Sample Input 1

0 
beast 
betas

Sample Output 1

1

Sample Input 2

1
aaaaa 
bbbbb

Sample Output 2

6

Giới hạn:

• Có 40% số test ứng với ~|S_1|=|S_2| ≤ 300~; ~k ≤ 25~
• Có 30% số test ứng với ~|S_1|=|S_2| ≤ 3000~; ~k = 0~
• Có 30% số test ứng với ~|S_1|=|S_2| ≤ 3000~; ~k ≤ 25~