Mô tả vấn đề

Snuke có một khuôn hình vuông kích thước ~ N \times N ~ ô.

Mỗi cạnh của hình vuông là một phần của chu vi được gắn một lỗ. Nghĩa là, mỗi bên của lưới được có với ~ N ~ lỗ trống, với tổng số ~ 4 \times N ~ lỗ. Các lỗ này được dán nhãn như sau:

• Các lỗ ở phía trên của lưới: ~ U1, U2, ..., UN ~ từ trái sang phải
• Các lỗ ở phía dưới của lưới: ~ D1, D2, ..., DN ~ từ trái sang phải
• Các lỗ ở phía bên trái của lưới: ~ L1, L2, ..., LN ~ từ trên xuống dưới
• Các lỗ ở phía bên phải của lưới: ~ R1, R2, ..., RN ~ từ trên xuống dưới

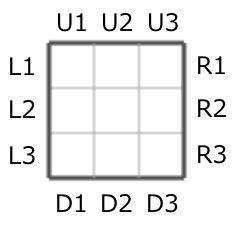Hình mô tả nhán đánh dấu các lỗ

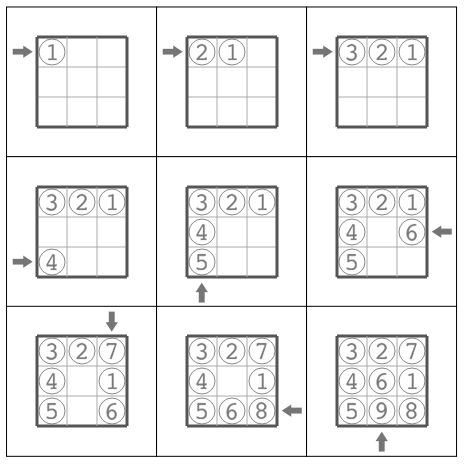
Snuke có thể chèn một viên gạch từ mỗi lỗ vào khuôn mà lỗ được gắn vào. Khi một ô bên trong đã bị chiếm, ô đang chiếm sẽ được đẩy sang ô tiếp theo và khi ô tiếp theo cũng bị chiếm bởi một ô khác, ô chiếm đó cũng sẽ được đẩy, v.v. Snuke không thể chèn một ô nếu nó sẽ dẫn đến một ô bị đẩy ra khỏi khuôn. Hành vi của các ô khi một ô được chèn được thể hiện chi tiết tại Đầu vào / Đầu ra Mẫu ~ 1 ~.

Snuke đang cố gắng chèn ~ N \times N ~ viên gạch lần lượt từ các ổ cắm để đạt được trạng thái mà mọi ô vuông đều chứa một viên gạch. Ở đây, anh ta phải chèn chính xác ~ U_i ~ viên gạch từ socket ~ Ui ~, ~ D_i ~ viên gạch từ socket ~ Di ~, ~ L_i ~ viên gạch từ socket ~ Li ~ và ~ R_i ~ viên gạch từ socket ~ Ri ~. Xác định xem có thể chèn các viên gạch mà không vượt quá hạn chế hay không. Nếu có thể, các viên gạch nên được lắp từ các ổ cắm theo thứ tự nào?

Hạn chế

• ~ 1 ≤ N ≤ 300 ~
• ~ U_i, D_i, L_i ~ và ~ R_i ~ là các số nguyên không âm.
• Tổng tất cả các giá trị ~ U_i, D_i, L_i ~ và ~ R_i ~ bằng ~ N \ lần N ~.

Input

Đầu vào được cung cấp từ Đầu vào chuẩn ở định dạng sau:

~ N ~

~ U_1 ~ ~ U_2 ~ ~ ... ~ ~ U_N ~

~ D_1 ~ ~ D_2 ~ ~ ... ~ ~ D_N ~

~ L_1 ~ ~ L_2 ~ ~ ... ~ ~ L_N ~

~ R_1 ~ ~ R_2 ~ ~ ... ~ ~ R_N ~

Output

Nếu có thể chèn các viên gạch sao cho mỗi ô vuông sẽ chứa một viên, hãy in nhãn của các ổ cắm theo thứ tự các ô sẽ được chèn từ chúng, mỗi ô trên một dòng. Nếu không thể, hãy in `NO ''. Nếu tồn tại nhiều hơn một giải pháp, hãy in bất kỳ giải pháp nào trong số đó.

Đầu vào Mẫu 1

3
0 0 1
1 1 0
3 0 1
0 1 1

Đầu ra Mẫu 1

L1
L1
L1
L3
D1
R2
U3
R3
D2

Snuke có thể chèn các ô như trong hình bên dưới. Mũi tên cho biết vị trí được chèn một ô, vòng tròn biểu thị một ô và một số được viết trong một vòng tròn cho biết có bao nhiêu ô được chèn trước đó.

Đầu vào Mẫu 2

2
2 0
2 0
0 0
0 0

Đầu ra mẫu 2

NO

Mô tả vấn đề

Takahashi đang chơi với thẻ ~ N ~.

Thẻ thứ ~ i ~ có một số nguyên ~ X_i ~ trên đó.

Takahashi đang cố gắng tạo ra nhiều cặp bài nhất có thể đáp ứng một trong các điều kiện sau:

• Các số nguyên trên hai thẻ giống nhau.
• Tổng các số nguyên trên hai thẻ là bội của ~ M ~.

Tìm số cặp tối đa có thể được tạo ra.

Lưu ý rằng một thẻ không thể được sử dụng trong nhiều cặp.

Hạn chế

• ~ 2 ≤N ≤ 10 ^ 5 ~
• ~ 1 ≤ M ≤ 10 ^ 5 ~
• ~ 1 ≤ X_i ≤ 10 ^ 5 ~

Input

Đầu vào được cung cấp theo định dạng sau:

~ N ~ ~ M ~

~ X_1 ~ ~ X_2 ~ ~ ... ~ ~ X_N ~

Output

In số lượng cặp tối đa có thể được tạo.

Đầu vào Mẫu 1

7 5
3 1 4 1 5 9 2

Đầu ra Mẫu 1

3

Ba cặp ~ (3,2), (1,4) ~ và ~ (1,9) ~ có thể được tạo.

Có thể tạo các cặp ~ (3,2) ~ và ~ (1,1) ~, nhưng số lượng cặp không phải là tối đa với điều này.

Đầu vào Mẫu 2

15 10
1 5 6 10 11 11 11 20 21 25 25 26 99 99 99

Đầu ra Mẫu 2

6

Mô tả vấn đề

Có ~ N ~ ô vuông liên tiếp, được đánh số từ ~ 1 ~ đến ~ N ~ từ trái sang phải. Snuke và Rng đang chơi trò chơi trên bàn cờ bằng cách sử dụng các ô vuông này, được mô tả dưới đây:

1. Đầu tiên, Snuke viết một số nguyên vào mỗi ô vuông.
2. Mỗi người trong hai người chơi sở hữu một mảnh. Snuke đặt quân cờ của mình vào ô vuông ~ 1 ~, và Rng đặt quân cờ vào ô vuông ~ 2 ~.
3. Người chơi có quân cờ ở bên trái đối phương sẽ di chuyển quân cờ của mình. Đích đến phải là một hình vuông ở bên phải của hình vuông nơi quân cờ đang được đặt và không được vào hình vuông nơi quân cờ của đối thủ được đặt.
4. Lặp lại bước 3. Khi các quân cờ không thể di chuyển được nữa, trò chơi kết thúc.
5. Điểm của mỗi người chơi được tính bằng tổng các số nguyên được viết trong các ô vuông mà người chơi đã đặt quân cờ của mình trước khi kết thúc trò chơi.

Snuke đã viết một số nguyên ~ A_i ~ vào hình vuông ~ i (1 ≤ i ≤ N-1) ~, nhưng không viết vào hình vuông thứ ~ N ~. Anh ấy đã quyết định tính toán cho mỗi ~ M ~ số nguyên ~ X_1, X_2, ..., X_M ~, nếu anh ấy viết nó vào ô vuông ~ N ~ và trò chơi được chơi, giá trị Điểm của Snuke - Điểm của Rng sẽ được là bao nhiêu. Ở đây, người ta giả định rằng mỗi người chơi di chuyển quân cờ của mình để tối đa hóa giá trị điểm của người chơi - điểm của đối thủ.

Hạn chế

• ~ 3 ≤ N ≤ 200.000 ~
• ~ 0 ≤ A_i ≤ 10 ^ 6 ~
• Tổng của tất cả ~ A_i ~ nhiều nhất là ~ 10 ^ 6 ~.
• ~ 1 ≤ M ≤ 200.000 ~
• ~ 0 ≤ X_i ≤ 10 ^ 9 ~

Đầu vào

Đầu vào được cung cấp theo định dạng sau:

~ N ~

~ A_1 ~ ~ A_2 ~ ~ ... ~ ~ A_ {N-1} ~

~ M ~

~ X_1 ~

~ X_2 ~

~: ~

~ X_M ~

Đầu ra

Đối với mỗi số nguyên ~ M ~ ~ X_1, ..., X_M ~, in ra giá trị "(Điểm của Snuke) - (Điểm của Rng)" nếu nó được viết thành ô vuông ~ N ~, một trên mỗi dòng.

Đầu vào Mẫu 1

5
2 7 1 8
1
2

Đầu ra Mẫu 1

0

Trò chơi diễn ra như sau, trong đó Sđại diện cho quân của Snuke vàR đại diện cho Rng.

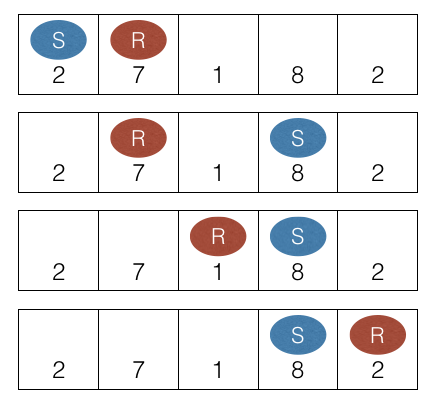
Điểm của cả hai người chơi là ~ 10 ~, do đó "(Điểm của Snuke) - (Điểm của Rng)" là ~ 0 ~.

Đầu vào Mẫu 2

9
2 0 1 6 1 1 2 6
5
2016
1
1
2
6

Đầu ra Mẫu 2

2001
6
6
7
7

Mô tả vấn đề

Trên một hành tinh xa, rất xa, ~ M ~ ngôn ngữ được sử dụng. Chúng được đánh số thuận tiện ~ 1 ~ đến ~ M ~.

Đối với CODE FESTIVAL 20XX được tổ chức trên hành tinh này, ~ N ~ người tham gia tập hợp từ khắp nơi trên hành tinh.

Người tham gia thứ ~ i ~ ~ (1 ≤ i ≤ N) ~ có thể nói ~ K_i ~ ngôn ngữ được đánh số ~ L_ {i, 1}, L_ {i, 2}, ..., L_ {i, {} K_i} ~.

Hai người tham gia ~ A ~ và ~ B ~ có thể kết hợp với nhau nếu và chỉ khi một trong các điều kiện sau được thoả mãn:

• Có một ngôn ngữ mà cả ~ A ~ và ~ B ~ đều có thể nói được.
• Có một người tham gia ~ X ~ mà cả ~ A ~ và ~ B ~ đều có thể giao tiếp.

Xác định xem tất cả ~ N ~ người tham gia có thể giao tiếp với tất cả những người tham gia khác hay không.

Hạn chế

• ~ 2 ≤ N ≤ 10 ^ 5 ~
• ~ 1 ≤ M ≤ 10 ^ 5 ~
• ~ 1 ≤ K_i ≤ M ~
• ~ (~ Tổng của tất cả ~ K_i) ≤ 10 ^ 5 ~
• ~ 1 ≤ L_ {i, j} ≤M ~
• ~ L_ {i, 1}, L_ {i, 2}, ..., L_ {i, {} K_i} ~ phân biệt theo từng cặp.

Input

Đầu vào được cung cấp từ Đầu vào chuẩn ở định dạng sau:

~ N ~ ~ M ~

~ K_1 ~ ~ L_ {1,1} ~ ~ L_ {1,2} ~ ~ ... ~ ~ L_ {1, {} K_1} ~

~ K_2 ~ ~ L_ {2,1} ~ ~ L_ {2,2} ~ ~ ... ~ ~ L_ {2, {} K_2} ~

~: ~

~ K_N ~ ~ L_ {N, 1} ~ ~ L_ {N, 2} ~ ~ ... ~ ~ L_ {N, {} K_N} ~

Output

Nếu tất cả ~ N ~ người tham gia có thể giao tiếp với tất cả những người tham gia khác, hãy in YES. Nếu không, hãy in NO.

Đầu vào Mẫu 1

4 6
3 1 2 3
2 4 2
2 4 6
1 6

Đầu ra Mẫu 1

YES

Hai người tham gia bất kỳ có thể liên lạc với nhau, như sau:

• Người tham gia ~ 1 ~ và ~ 2 ~: cả hai đều có thể nói ngôn ngữ ~ 2 ~.
• Người tham gia ~ 2 ~ và ~ 3 ~: cả hai đều có thể nói ngôn ngữ ~ 4 ~.
• Người tham gia ~ 1 ~ và ~ 3 ~: cả hai đều có thể giao tiếp với người tham gia ~ 2 ~.
• Người tham gia ~ 3 ~ và ~ 4 ~: cả hai đều có thể nói ngôn ngữ ~ 6 ~.
• Người tham gia ~ 2 ~ và ~ 4 ~: cả hai đều có thể giao tiếp với người tham gia ~ 3 ~.
• Người tham gia ~ 1 ~ và ~ 4 ~: cả hai đều có thể giao tiếp với người tham gia ~ 2 ~.

Lưu ý rằng có thể không có người tham gia nói ngôn ngữ nào.

Đầu vào Mẫu 2

4 4
2 1 2
2 1 2
1 3
2 4 3

Đầu ra Mẫu 2

NO

Ví dụ, những người tham gia ~ 1 ~ và ~ 3 ~ không thể giao tiếp với nhau.

Mô tả vấn đề

Chúng ta có một đồ thị với ~ N ~ đỉnh, được đánh số từ ~ 0 ~ đến ~ N-1 ~. Các cạnh vẫn chưa được thêm vào.

Chúng tôi sẽ xử lý các truy vấn ~ Q ~ để thêm các cạnh. Trong truy vấn ~ i ~ -th ~ (1 ≤ i ≤ Q) ~, ba số nguyên ~ A_i, B_i ~ và ~ C_i ~ sẽ được đưa ra và chúng ta sẽ thêm vô số cạnh vào biểu đồ như sau:

• Hai đỉnh được đánh số ~ A_i ~ và ~ B_i ~ sẽ được nối với nhau bằng một cạnh có trọng số là ~ C_i ~.
• Hai đỉnh được đánh số ~ B_i ~ và ~ A_i + 1 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 1 ~.
• Hai đỉnh được đánh số ~ A_i + 1 ~ và ~ B_i + 1 ~ sẽ được nối với nhau bởi một cạnh có trọng số ~ C_i + 2 ~.
• Hai đỉnh được đánh số ~ B_i + 1 ~ và ~ A_i + 2 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 3 ~.
• Hai đỉnh được đánh số ~ A_i + 2 ~ và ~ B_i + 2 ~ sẽ được nối với nhau bởi một cạnh có trọng số ~ C_i + 4 ~.
• Hai đỉnh được đánh số ~ B_i + 2 ~ và ~ A_i + 3 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 5 ~.
• Hai đỉnh được đánh số ~ A_i + 3 ~ và ~ B_i + 3 ~ sẽ được nối với nhau bằng một cạnh có trọng số ~ C_i + 6 ~.
• ...

Ở đây, hãy xem xét các chỉ số của các đỉnh modulo ~ N ~. Ví dụ, đỉnh được đánh số ~ N ~ là một được đánh số ~ 0 ~, và đỉnh được đánh số ~ 2N-1 ~ là một được đánh số ~ N-1 ~.

Hình dưới đây cho thấy bảy cạnh đầu tiên được thêm vào khi ~ N = 16, A_i = 7, B_i = 14, C_i = 1 ~:

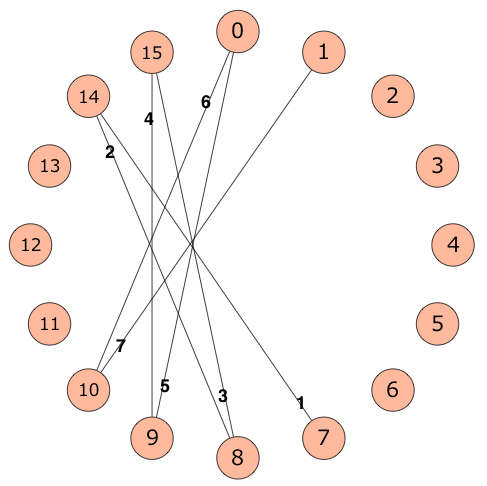
Sau khi xử lý tất cả các truy vấn, hãy tìm tổng trọng số của các cạnh có trong cây khung tối thiểu của đồ thị.

Hạn chế

• ~ 2 ≤ N ≤ 200.000 ~
• ~ 1 ≤ Q ≤ 200.000 ~
• ~ 0 ≤ A_i, B_i ≤ N-1 ~
• ~ 1 ≤ C_i ≤ 10 ^ 9 ~

Input

Đầu vào được cung cấp từ Đầu vào chuẩn ở định dạng sau:

~ N ~ ~ Q ~

~ A_1 ~ ~ B_1 ~ ~ C_1 ~

~ A_2 ~ ~ B_2 ~ ~ C_2 ~

~ A_Q ~ ~ B_Q ~ ~ C_Q ~

Output

In tổng trọng lượng của các cạnh có trong cây khung tối thiểu của biểu đồ.

Đầu vào Mẫu 1

7 1
5 2 1

Đầu ra Mẫu 1

21

Hình dưới đây cho thấy cây khung tối thiểu của biểu đồ:

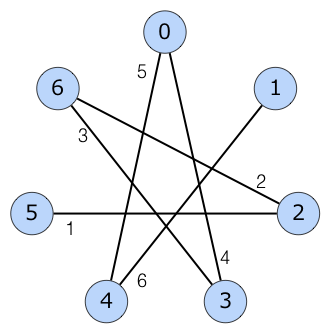
Lưu ý rằng có thể có nhiều cạnh nối cùng một cặp đỉnh.

Đầu vào Mẫu 2

2 1
0 0 1000000000

Đầu ra Mẫu 2

1000000001

Cũng lưu ý rằng có thể có các vòng lặp tự.

Đầu vào Mẫu 3

5 3
0 1 10
0 2 10
0 4 10

Đầu ra mẫu 3

42

Mô tả vấn đề

Rng đang nướng bánh quy.

Ban đầu, anh ta có thể nướng một chiếc bánh quy một giây.

Anh ấy cũng có thể ăn bánh quy do chính mình nướng. Khi còn ~ x ~ bánh quy chưa ăn, anh ta có thể chọn ăn tất cả bánh quy đó. Sau khi anh ta ăn xong những chiếc bánh quy đó, số lượng bánh anh ta có thể nướng mỗi giây trở thành ~ x ~. Lưu ý rằng một chiếc bánh quy luôn cần được nướng trong ~ 1 ~ giây, tức là anh ta không thể nướng một chiếc bánh quy trong ~ 1 / x ~ giây khi ~ x> 1 ~. Khi anh ta chọn ăn bánh, anh ta phải ăn tất cả chúng; anh ta không thể chọn chỉ ăn một phần của chúng. Anh ta phải mất ~ A ~ giây để ăn bánh quy bất kể số lượng bao nhiêu, trong thời gian đó không có bánh quy nào có thể nướng được.

Anh ấy muốn tặng ~ N ~ bánh quy cho bà. Tìm khoảng thời gian ngắn nhất cần thiết để sản xuất ít nhất ~ N ~ bánh quy chưa được ăn.

Hạn chế

• ~ 1 ≤ N ≤ 10 ^ {12} ~
• ~ 0 ≤ A ≤ 10 ^ {12} ~
• ~ A ~ là một số nguyên.

Input

Đầu vào được cung cấp theo định dạng sau:

~ N ~ ~ A ~

Output

In trong thời gian ngắn nhất cần thiết để tạo ra ít nhất ~ N ~ bánh quy chưa ăn.

Đầu vào Mẫu 1

8 1

Đầu ra Mẫu 1

7

Có thể tạo ra ~ 8 ~ cookie trong ~ 7 ~ giây, như sau:

• Sau ~ 1 ~ giây: ~ 1 ~ cookie được hoàn thành.
• Sau ~ 2 ~ giây: ~ 1 ~ cookie nữa được hoàn thành, tổng cộng ~ 2 ~. Bây giờ, Rng bắt đầu ăn ~ 2 ~ bánh quy đó.
• Sau ~ 3 ~ giây: Anh ấy ăn xong bánh quy và giờ anh ấy có thể nướng ~ 2 ~ bánh quy mỗi giây.
• Sau ~ 4 ~ giây: ~ 2 ~ cookie được hoàn thành.
• Sau ~ 5 ~ giây: ~ 2 ~ cookie nữa được hoàn thành, tổng cộng ~ 4 ~.
• Sau ~ 6 ~ giây: ~ 2 ~ cookie nữa được hoàn thành, tổng cộng ~ 6 ~.
• Sau ~ 7 ~ giây: ~ 2 ~ cookie nữa được hoàn thành, tổng cộng ~ 8 ~.

Đầu vào Mẫu 2

1000000000000 1000000000000

Đầu ra Mẫu 2

1000000000000

Mô tả vấn đề

Vấn đề được đặt ra tại CODE FESTIVAL 20XX Finals bao gồm ~ N ~ vấn đề.

Điểm được phân bổ cho vấn đề thứ ~i~ ~ (1 ≤ i ≤ N) ~ là ~ i ~ điểm.

Nam, một thí sinh, đang cố gắng ghi chính xác ~ N ~ điểm. Vì vậy, anh ấy đang quyết định vấn đề nào cần giải quyết.

Vì các bài toán có điểm cao hơn khó hơn, anh ấy muốn giảm thiểu điểm cao nhất của một bài toán trong số các bài do anh ấy giải được.

Xác định tập hợp các vấn đề cần được giải quyết.

Hạn chế

• ~ 1 ≤ N ≤ 10 ^ 7 ~

Input

Đầu vào được cung cấp theo định dạng sau:

~ N ~

Output

Trong số các tập hợp bài toán có tổng điểm là ~ N ~, hãy tìm một tập hợp trong đó điểm cao nhất của một bài toán là nhỏ nhất, sau đó in chỉ số của các bài toán trong tập hợp theo thứ tự bất kỳ, một trên mỗi dòng.

Nếu tồn tại nhiều hơn một bộ như vậy, bất kỳ bộ nào trong số chúng sẽ được chấp nhận.

Đầu vào Mẫu 1

4

Đầu ra Mẫu 1

1
3

Chỉ giải bài toán thứ 4 cũng sẽ dẫn đến tổng điểm là ~ 4 ~ điểm, nhưng giải bài toán thứ 1 và thứ 3 sẽ làm giảm điểm cao nhất của bài toán đã giải.

Đầu vào Mẫu 2

7

Đầu ra Mẫu 2

1
2
4

Tập hợp ~ \\ {3,4 \\} ~ cũng sẽ được chấp nhận.

Đầu vào Mẫu 3

1

Đầu ra mẫu 3

1

Mô tả vấn đề

Có ~ N ~ thị trấn ở Vương quốc Takahashi. Chúng được đánh số ~ 1 ~ đến ~ N ~.

Nhà vua Takahashi đang có kế hoạch đi thị sát trong ~ M ~ ngày. Anh ta sẽ xác định một chuỗi các thị trấn ~ c ~, và đến thăm thị trấn ~ c_i ~ vào ngày thứ ~ i ~. Tức là, vào ngày thứ ~ i ~, anh ấy sẽ đi từ vị trí hiện tại của mình đến thị trấn ~ c_i ~. Nếu anh ấy đã ở thị trấn rồi ~ c_i ~, anh ấy sẽ ở lại thị trấn đó. Vị trí của anh ấy ngay trước khi bắt đầu chuyến tham quan là thị trấn ~ 1 ~, thủ đô. Chuyến tham quan kết thúc tại thị trấn ~ c_M ~ mà không cần quay lại thủ đô.

Vấn đề là không có con đường trải nhựa ở vương quốc này. Anh quyết định giải quyết vấn đề này bằng cách tự mình mở đường khi đi du lịch. Khi anh ta đi từ thị trấn ~ a ~ đến thị trấn ~ b ~, sẽ có một con đường một chiều mới được trải nhựa từ thị trấn ~ a ~ đến thị trấn ~ b ~.

Vì anh ấy quan tâm đến người dân của mình, anh ấy muốn điều kiện sau được thỏa mãn sau khi chuyến hành trình của anh ấy kết thúc: "có thể đi từ bất kỳ thị trấn nào đến bất kỳ thị trấn nào khác bằng cách đi qua những con đường do anh ấy trải nhựa". Có bao nhiêu chuỗi ~ c ~ thỏa mãn điều kiện này?

Hạn chế

• ~ 2 ≤ N ≤ 300 ~
• ~ 1 ≤ M ≤ 300 ~

Input

Đầu vào được cung cấp theo định dạng sau:

~ N ~ ~ M ~

Output

In số chuỗi các thị trấn thỏa mãn điều kiện, modulo ~ 1000000007 (= 10 ^ 9 + 7) ~.

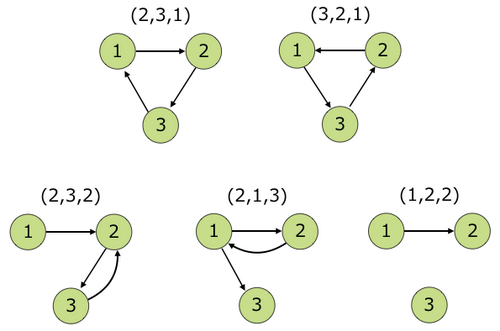
Đầu vào Mẫu 1

3 3

Đầu ra Mẫu 1

2

Như hình dưới đây, điều kiện chỉ được thỏa mãn khi ~ c = (2,3,1) ~ hoặc ~ c = (3,2,1) ~. Các dãy như ~ c = (2,3,2) ~, ~ c = (2,1,3) ~, ~ c = (1,2,2) ~ không thỏa mãn điều kiện.

Đầu vào Mẫu 2

150 300

Đầu ra Mẫu 2

734286322

Đầu vào Mẫu 3

300 150

Đầu ra mẫu 3

0

Mô tả vấn đề

Có một lưới với ~H~ hàng and ~W~ cột.

Ô ở hàng thứ i và cột thứ j chứa một chuỗi ~S_{i,j}~ có độ dài là ~5~ .

Các hàng được đánh số từ ~1~ đến ~H~ , và các cột được đánh dấu bằng các chứ cái tiếng Anh viết hoa từ A đến ký tự thứ ~W~ trong bảng chữ cái.

Có chính xác một ô trong lưới chứa chuỗi snuke . Tìm chuỗi này trong lưới và thông báo vị trí của nó.

Ví dụ, ô ở hàng thứ 6 và cột thứ 8 là H6 .

Ràng buộc cho vấn đề:

• ~1≦H, W≦26~
• Độ dài của chuỗi ~S_{i,j}~ là ~5~ .
• ~S_{i,j}~ chứa các ký tự tiếng anh viết thường ( a - z ).
• Có chính xác một chuỗi trong lưới là snuke .

Input

Đầu vào được cung cấp theo định dạng sau:

~H~ ~W~

~S_{1,1}~ ~S_{1,2}~ ~...~ ~S_{1,W}~

~S_{2,1}~ ~S_{2,2}~ ~...~ ~S_{2,W}~

~:~

~S_{H,1}~ ~S_{H,2}~ ~...~ ~S_{H,W}~

Output

In ra vị trí của chuỗi snuke trong lưới, không chứa ký tự dấu cách ở giữa.

Sample Input 1

15 10
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snuke snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake
snake snake snake snake snake snake snake snake snake snake

Sample Output 1

H6

Sample Input 2

1 1
snuke

Sample Output 2

A1

Báo cáo vấn đề

Snuke có một lưới với ~ H ~ hàng và ~ W ~ cột. Hình vuông ở hàng ~ i ~ -th và cột ~ j ~ -th chứa ký tự ~ S_ {i, j} ~.

Anh ta có thể thực hiện hai loại hoạt động sau trên lưới:

• Đảo ngược thứ tự của các ô vuông trong một hàng đã chọn.
• Đảo ngược thứ tự của các ô vuông trong một cột đã chọn.

Ví dụ: đảo ngược hàng thứ ~ 2 ~ , sau đó đảo ngược cột thứ ~ 4 ~ sẽ cho kết quả như sau:

Bằng cách thực hiện các thao tác này bất kỳ số lần nào theo thứ tự bất kỳ, có thể thu được bao nhiêu vị trí của ký tự trên lưới?

Hạn chế

• ~ 1 ≦ H, W ≦ 200 ~
• ~ S_ {i, j} ~ là một chữ cái tiếng Anh viết thường (a - z).

Đầu vào

Đầu vào được cung cấp từ Đầu vào chuẩn ở định dạng sau:

~ H ~ ~ W ~

~ S_ {1,1} ~ ~ S_ {1,2} ~ ~ ... ~ ~ S_ {1, W} ~

~ S_ {2,1} ~ ~ S_ {2,2} ~ ~ ... ~ ~ S_ {2, W} ~

~: ~

~ S_ {H, 1} ~ ~ S_ {H, 2} ~ ~ ... ~ ~ S_ {H, W} ~

Đầu ra

In số lượng vị trí ký tự trên lưới có thể nhận được, modulo ~ 1000000007 (= 10 ^ 9 + 7) ~.

Đầu vào Mẫu 1

2 2
cf
cf

Đầu ra Mẫu 1

6

Có thể nhận được ~ 6 ~ vị trí ký tự sau:

Đầu vào Mẫu 2

1 12
codefestival

Đầu ra Mẫu 2

2