Tôi có ~n~ người bạn là những con số, họ đang chơi một trò chơi nho nhỏ bằng việc bắt đầu xếp thành một hàng từ bé đến lớn. Vì tôi có quá nhiều người bạn nhưng tầm mắt của tôi không xa đến thế, tôi cần bạn giúp tôi bằng cách với mỗi câu hỏi của tôi, hãy cho biết cậu ta đang ở đứng tại đâu trong hàng.

Để thuận tiện, tôi sẽ luôn đếm vị trí đầu tiên từ số ~1~. Hãy tìm các bạn của tôi, và tôi sẽ cho bạn dấu tick màu xanh lá.

Input

• Dòng đầu tiên là số nguyên ~n~ là số người bạn tôi có.
• Dòng thứ hai gồm ~n~ số nguyên dương. Số thứ ~i~ là ~A_i~, người bạn thứ ~i~ của tôi (~1 \leq n \leq 2 \cdot 10^5~, ~1 \leq A_i \leq 10^9~).
• Dòng thứ ba là số nguyên ~q~ là số câu hỏi tôi có (~1 \leq q \leq 10^5~).
• ~q~ dòng tiếp theo, mỗi dòng ghi một số nguyên dương không quá ~10^9~ cho biết người bạn tôi cần tìm.

Tôi đảm bảo những người bạn của tôi đã xếp hàng theo thứ tự từ bé đến lớn, cũng như đều đôi một khác nhau về giá trị.

Output

Ghi ra ~q~ dòng, dòng thứ ~i~ tương ứng với câu trả lời cho câu hỏi thứ ~i~. Nếu không tìm thấy xin hãy ghi -1.

Sample input

5
1 4 9 16 25
3
1
16
0

Sample output

1
4
-1

Cho một dãy ~A~, đếm số lượng số trong dãy mang giá trị trong khoảng ~[l, r]~.

Input

• Dòng đầu tiên là số nguyên ~n~ cho biết số phần tử của dãy ~A~.
• Dòng thứ hai gồm ~n~ số nguyên dương, số thứ ~i~ ghi giá trị của phần tử ~A_i~ (~1 \leq n \leq 2 \cdot 10^5~, ~1 \leq A_i \leq 10^9~).
• Dòng thứ ba là số nguyên ~q~ là số lượng truy vấn (~1 \leq q \leq 2 \cdot 10^5~).
• ~q~ dòng tiếp theo, dòng thứ ~i~ ghi hai số nguyên dương ~l_i~, ~r_i~ (~1 \leq l_i \leq r_i \leq 10^9~).

Output

Ghi ra ~q~ dòng, dòng thứ ~i~ tương ứng với câu trả lời cho truy vấn thứ ~i~.

Sample input

5
1 4 9 16 25
3
1 2
1 30
10 15

Sample output

1
5
0

Subtask

• ~30\%~ số test có ~1 \leq n, q \leq 10^3~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Một nghiên cứu gần đây cho thấy những chú hải cẩu, với thân hình to lớn của mình, rất tự hào và coi trọng về cân nặng của chúng. Vì thế, những con hải cẩu thường tụm lại thành nhóm với những con khác có cân nặng tương đồng với nó. Nghiên cứu cũng chỉ ra thêm rằng bầy hải cẩu thường tách riêng ra thành các nhóm dễ gần, một nhóm gồm ~3~ con hải cẩu, trong đó chênh lệch cân nặng giữa hai con bất kỳ không quá ~10 \text{kg}~.

Tiến sĩ Minh, một nhà hải cẩu học lỗi lạc, đang cần nghiên cứu sâu hơn về tập tính sinh hoạt và chia nhóm của các con hải cẩu, vì thế cậu ấy cần phải chọn ra một nhóm dễ gần để thuận tiện nghiên cứu. Với một bầy gồm ~n~ con hải cẩu đang có sẵn trong trạm nghiên cứu của mình, cậu ấy có thể chọn ra bao nhiêu nhóm hải cẩu dễ gần để nghiên cứu?

Input

• Dòng đầu tiên là số nguyên ~n~ cho biết số con hải cẩu trong bầy của Minh.
• Dòng thứ hai gồm ~n~ số nguyên dương, số thứ ~i~ ghi giá trị của phần tử ~A_i~ là cân nặng của con hải cẩu thứ ~i~ (~1 \leq n \leq 2 \cdot 10^5~, ~1 \leq A_i \leq 10^9~).

Output

Ghi ra một số duy nhất cho biết số cách chọn nhóm hải cẩu mà Minh có thể chọn.

Sample input

5
1 2 4 8 12

Sample output

7

Subtask

• ~30\%~ số test có ~1 \leq n \leq 10^3~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Tìm ~x~ nguyên bé nhất sao cho ~\sqrt[3]{x} + \sqrt[4]{x} > N~.

Gợi ý: ~\sqrt[a]{n}~ có thể được tính bằng cách gọi pow(n, 1.0 / a).

Input

Gồm một dòng duy nhất ghi số nguyên dương ~N~ (~1 \leq N \leq 1000~).

Output

Ghi ra một số nguyên ~x~ duy nhất là đáp án cho đề bài.

Từ giới hạn đề bài có thể cho thấy giá trị của ~x~ luôn nằm vừa trong kiểu dữ liệu 32-bit.

Sample input

10

Sample output

229

Subtask

• ~30\%~ số test có ~1 \leq x \leq 10^6~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Minh đang sắp đón chào một chú hải cẩu mới về trạm nghiên cứu tại cực Bắc của mình, nơi mà cậu sẽ phải đưa nó đi qua các khu trong trạm để tới nơi ở mới của nó. Tại trạm của cậu, cơ sở vật chất đã cũ mà bầy hải cẩu con nào con nấy lại đều to béo, nên cậu khá lo khi việc đưa thêm một bé nặng trĩu đi ngang qua nữa có thể khiến lớp băng dưới khu đó nứt ra!

Cụ thể hơn, trạm của Minh gồm các khu xếp thành một bảng ~M \cdot N~ đánh số từ 1 theo thứ tự từ trên xuống và từ trái qua, khu ở hàng ~i~ cột ~j~ có thể chịu thêm sức nặng tối đa là ~A_{i, j}~. Cậu cần đưa nó đến khu ~(M, N)~ từ cổng vào trạm ở vị trí ~(1, 1)~, ở mỗi khu cậu có thể qua các khu kề cạnh khu hiện tại. Liệu chú hải cẩu này có thể có cân nặng tối đa là bao nhiêu để Minh có thể đưa nó an toàn đến khu của nó?

Input

• Dòng đầu tiên gồm 2 số nguyên dương ~M~, ~N~ cho biết độ lớn của trạm nghiên cứu. (~1 \leq M, N \leq 10^3~).
• ~M~ dòng tiếp theo, mỗi dòng ghi ~N~ số nguyên dương là sức chịu của từng khu (~1 \leq A_{i, j} \leq 10^9~).

Output

Ghi ra một số duy nhất cho biết cân nặng tối đa của chú hải cẩu mà Minh có thể mang theo.

Sample input

3 3
1 2 3
4 5 6
7 8 9

Sample output

1

Subtask

• ~30\%~ số test có ~1 \leq M, N \leq 3~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Trong khi phòng của Minh trong trạm nghiên cứu đã treo đầy tranh, những khu sinh sống của các con hải cẩu vẫn còn khá trống trải, nên cậu định treo thêm tranh vào các khu ấy. Khổ nỗi, do các thành tường của khu hay có tuyết nên chúng thường quá trơn trượt để có thể giữ được tranh, nên cậu quyết định làm thêm khung gỗ gắn phía sau của các bức tranh.

Cậu có ~N~ bức tranh hình vuông để treo, bức tranh thứ ~i~ có cạnh là ~A_i\text{ cm}~. Với mỗi bức tranh, cậu sẽ đóng khung tranh là một khối vuông lớn, rồi đặt các bức tranh lên sao cho viền của khung cách viền của bức tranh ~w\text{ cm}~. Sau khi đóng xong thì Minh nhận thấy cậu đã dùng hết ~c\text{ cm}^2~ gỗ.

Với kích thuớc của từng bức tranh và diện tích gỗ ~c~ đã dùng, bạn có tính được kích thước viền ~w~ của các khung tranh không?

Input

• Dòng đầu tiên gồm 2 số nguyên dương ~N~ và ~c~ (~1 \leq N \leq 2 \cdot 10^5~, ~1 \leq c \leq 10^{12}~) lần lượt là số lượng bức tranh và diện tích gỗ đã sử dụng.
• Dòng tiếp theo gồm ~N~ số, số thứ ~i~ ghi giá trị ~A_i~ (~1 \leq A_i \leq 10^3~) là độ dài cạnh của bức tranh thứ ~i~.

Output

Ghi ra một số nguyên dương ~w~ duy nhất là độ dài viền của các khung tranh.

Sample input

3 50
3 2 1

Sample output

1

Subtask

• ~30\%~ số test có ~1 \leq N \leq 10^3~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Điểm khác biệt duy nhất giữa bản dễ và bản khó của bài toán là giới hạn của ~N~.

Ở những nơi tuyết rơi quanh năm như cực Bắc, hình dạng của những bông tuyết không khỏi khiến bản chất tò mò của các nhà nghiên cứu nơi đây trỗi dậy. Từ cửa sổ của trạm nghiên cứu, Minh nhìn những bông tuyết lục giác rơi khi cậu chợt nghĩ rằng, tại sao một bông tuyết lại phải là ~6~-giác mà không phải là ~k~-giác bất kỳ? Thế là cậu xây dựng một mô hình toán học để miêu tả các bông tuyết ~k~-giác như sau:

• Bắt đầu dựng bông tuyết từ ~1~ ngọn duy nhất.
• Sau đó, từ ngọn đầu tiên nối vào nó thêm ~k~ ngọn và lặp lại bước này với mỗi ngọn được thêm. Để hình dạng dựng nên trông như một bông tuyết thực sự, bước này được lặp lại ít nhất ~2~ lần và với ~k > 1~.

Bên dưới là một bông tuyết ~4~-giác với kích thước tối thiểu:

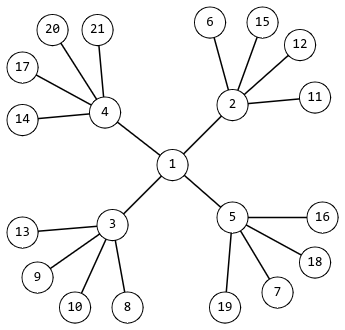
Để có thể hình dung được bông tuyết, cậu liền mang ~N~ con hải cẩu trong trạm của mình ra để xếp thử, nhưng với quy luật trên thì đôi khi một số lượng ngọn sẽ không thể dựng được một bông tuyết hoàn chỉnh. Liệu với ~N~ con hải cẩu Minh có thể dựng được một bông tuyết ~k~-giác hoàn chỉnh nào hay không?

Input

• Dòng đầu tiên gồm số nguyên dương ~Q~ (~1 \leq Q \leq 10^4~) là số lượng truy vấn bạn cần trả lời.
• ~Q~ dòng tiếp theo, mỗi dòng ghi một số nguyên dương ~N~ duy nhất (~1 \leq N \leq 10^6~).

Output

Gồm ~Q~ dòng, với mỗi dòng ghi YES hoặc NO là câu trả lời cho truy vấn đó.

Sample input

9
1
2
3
6
13
15
255
10101
1000000

Sample output

NO
NO
NO
NO
YES
YES
YES
YES
NO

Subtask

• ~30\%~ số test có ~1 \leq N \leq 10^3~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.

Điểm khác biệt duy nhất giữa bản dễ và bản khó của bài toán là giới hạn của ~N~.

Ở những nơi tuyết rơi quanh năm như cực Bắc, hình dạng của những bông tuyết không khỏi khiến bản chất tò mò của các nhà nghiên cứu nơi đây trỗi dậy. Từ cửa sổ của trạm nghiên cứu, Minh nhìn những bông tuyết lục giác rơi khi cậu chợt nghĩ rằng, tại sao một bông tuyết lại phải là ~6~-giác mà không phải là ~k~-giác bất kỳ? Thế là cậu xây dựng một mô hình toán học để miêu tả các bông tuyết ~k~-giác như sau:

• Bắt đầu dựng bông tuyết từ ~1~ ngọn duy nhất.
• Sau đó, từ ngọn đầu tiên nối vào nó thêm ~k~ ngọn và lặp lại bước này với mỗi ngọn được thêm. Để hình dạng dựng nên trông như một bông tuyết thực sự, bước này được lặp lại ít nhất ~2~ lần và với ~k > 1~.

Bên dưới là một bông tuyết ~4~-giác với kích thước tối thiểu:

Để có thể hình dung được bông tuyết, cậu liền mang ~N~ con hải cẩu trong trạm của mình ra để xếp thử, nhưng với quy luật trên thì đôi khi một số lượng ngọn sẽ không thể dựng được một bông tuyết hoàn chỉnh. Liệu với ~N~ con hải cẩu Minh có thể dựng được một bông tuyết ~k~-giác hoàn chỉnh nào hay không?

Input

• Dòng đầu tiên gồm số nguyên dương ~Q~ (~1 \leq Q \leq 10^4~) là số lượng truy vấn bạn cần trả lời.
• ~Q~ dòng tiếp theo, mỗi dòng ghi một số nguyên dương ~N~ duy nhất (~1 \leq N \leq 10^{12}~).

Output

Gồm ~Q~ dòng, với mỗi dòng ghi YES hoặc NO là câu trả lời cho truy vấn đó.

Sample input

9
1
2
3
6
13
15
255
10101
1000000

Sample output

NO
NO
NO
NO
YES
YES
YES
YES
NO

Một cặp số giai thừa của một số ~N~ là một cặp ~(x, y)~ nguyên dương bất kỳ sao cho ~x > y~ và

$$ \frac{x!}{y!} = N $$

Với một số ~N~ cho trước, hãy đưa ra một cặp số giai thừa ~(x, y)~ của ~N~ sao cho ~x~ bé nhất có thể.

Input

• Dòng đầu tiên gồm số nguyên dương ~Q~ (~1 \leq Q \leq 10^5~) là số lượng truy vấn bạn cần trả lời.
• ~Q~ dòng tiếp theo, mỗi dòng ghi một số nguyên dương ~N~ duy nhất (~2 \leq N \leq 10^9~).

Output

Với mỗi truy vấn ghi lần lượt hai số nguyên dương ~x~, ~y~ trên một dòng cho biết cặp số thoả điều kiện đề bài.

Có thể chứng minh rằng đáp án luôn tồn tại với giới hạn của đề bài.

Sample input

2
12
42

Sample output

4 2
7 5

Subtask

• ~30\%~ số test có ~1 \leq Q, N \leq 100~.
• ~70\%~ số test còn lại không có điều kiện gì thêm.